May 2001 Volume 23 Number 2

An Evaluation of Silica Gel for Humidity Control in Display Cases

Introduction

Museums are faced with the challenge of preserving artifacts for the enjoyment and education of current and future generations. The wide variety of artifacts that museums display requires maintaining specific environmental conditions to minimize their deterioration. Proper relative humidity (RH) control is one of the most important environmental factors in artifact preservation.

Conservation research has shown that RH levels above 65% will promote microbial growth (primarily fungi), while RH levels below 25% can lead to brittleness and cracking. In addition, large fluctuations in RH can lead to dimensional changes, deformation, and mechanical stress in organic materials. Though there is still debate about the appropriate RH requirements for museum environments, a set point of 50% (or the historic building average) with allowable fluctuations of ±5-10% is a generally accepted guideline.

Though mechanical humidification systems for RH control are common, many museums do not use them due to factors such as cost and the difficulty integrating them with the existing building structure and aesthetics. An alternate method of RH control that is employed in many museums is the use of an adsorbent material in combination with a well-sealed display case to create a micro-environment that serves to mitigate the large RH fluctuations that the general building environment may experience.

The most commonly used adsorbent is silica gel due to its high water capacity, chemical inertness, and ability to undergo an indefinite number of moisture cycles. This method has been prescribed in the conservation literature for many years, most notably by Thomson (1977) who developed the idea of 'hygrometric half-time,' t1/2, as the time it takes for the RH inside a case to reach the halfway point of the ambient RH. The hygrometric half time is calculated by the following equation:

Thomson calls M the 'specific moisture reservoir' of the buffering material. M is defined as the mass of water (grams of water) gained or lost per unit mass of adsorbent media (one kilogram of buffering material) for a 1% change in RH. The M-value is essentially the slope of the buffering material's adsorption isotherm evaluated at a specific RH, and it describes the incremental moisture buffering capacity of a material. In order to provide effective RH control, the adsorbent material must have a high M-value over the acceptable RH range for a given artifact. Increasing the M-value reduces the amount of adsorbent required to achieve proper control.

According to Thomson, the hygrometric half time is dependent upon two main factors: (1) the air leakage rate of the case, N and (2) the amount of the buffering material inside the case, B. B will be referred to as the gel sizing factor; it is the dry mass of buffering material in kg per cubic meter of case volume. By decreasing the air leakage rate or increasing the amount of buffering material, the hygrometric half time is increased, and greater RH control inside the case can be achieved.

Thomson states that a well-sealed case can be expected to have an air leakage rate of one air change per day. Using Eq.1 Thomson calculates that 20 kg/m³ (1.25 lb/ft³) of silica gel with an M-value of 2 g/kg would be needed to achieve a hygrometric half-time of 150 days for a display case having a leakage rate of 1 air change per day (ACD). This recommendation has become the standard guideline for using silica gel as a passive RH control method inside display cases.

Previous studies, e.g., Guinchen and Gai (1984), Schweizer (1984), Stolow (1977), have found silica gel to be an effective method of RH control inside display cases. However, in a recent research project evaluating the environmental conditions at the Field Museum of Natural History in Chicago a silica gel application was found to be ineffective at controlling the RH inside a newly-constructed display case.

The case had a volume of 1.7 m³ (60 ft³) and contained Chinese wood and ivory carvings. Three cassettes, each containing 750 grams (1.65 lbs) of Art-Sorb, were located in drawers at the bottom of the case. The Art-Sorb was conditioned to a relative humidity of 45% prior to being placed inside the case. Figure 1 shows the relative humidity levels measured inside and outside the case over a two-month period from February to April of 1999. The Art-Sorb had no discernible buffering effect with the relative humidity levels inside the case being almost the same as the ambient levels and well below the desired level of 45%.

Figure 1. Comparison of RH levels inside a display case containing Art-Sorb with ambient building levels at the Field Museum of Natural History in Chicago, Illinois.

This experience became a motivating factor for the present study. The goal of this study was to evaluate the effectiveness of silica gel for use in controlling RH levels inside display cases. The study consisted of the following parts:

• experimentally determine the adsorption and desorption isotherms of the three silica gels
• develop a mathematical model of the solid adsorbent media for passive RH control in a display case application
• experimentally validate the model
• use computer simulations to evaluate the effect of varying building and case conditions on silica gel performance.

Three silica gels were evaluated in the study. They were generic regular density silica gel, which is available from many chemical supply companies, and two specialty gels marketed specifically for museum conservation applications: Artengel and Art-Sorb.

Experimental Measurement of Adsorption and Desorption Isotherms

The adsorption and desorption isotherms describe the equilibrium moisture concentration (EMC) of a material at different RH levels.

The isotherms of the three gels were measured experimentally by allowing samples to come into equilibrium at different RH levels inside a constructed humidity chamber and measuring their weight gain in water. Equilibrium was attained when the measured weight of the gel samples did not change over time.

The isotherms were measured three times to verify their accuracy. Weight measurements were made with a Sartorius L420 S top-loading laboratory scale (accuracy ±0.0005 g) which was located in the humidity chamber. Different RH levels were achieved using the saturated salt solutions listed in Table 1, the work of Greenspan (1977).

The RH inside the chamber was measured using a Hobo H8 Pro Series Temp/RH data-logging sensor with a stated manufacturer's accuracy of ±3% RH and ±0.3°C. An isotherm set was also measured using a high accuracy General Eastern Hygro M-1 dew point hygrometer (accuracy �0.2°C).

Experimental Isotherm Data

Table 2 shows the experimental adsorption and desorption isotherm data for the three gels. All the data were obtained at temperatures between 23-25°C. The EMC of each gel is expressed as a percentage of the gel's dry weight, so an EMC of 20% means that the gel would be able to hold an amount of water equal to 20% of its dry weight.

The experimental isotherm data were fitted to the Dubinin-Astakhov (D-A) (1977) equation using a non-linear least squares method. The D-A equation expresses the equilibrium moisture concentration of the gel as a function of the adsorption potential, A defined as:

The Dubinin-Astakhov equation is given by:

EMC%=q x 100 (Eq. 4)

where q0, q1, E0, E1, n1, and n2 are equation parameters.

Figures 2-4 compare the isotherm's curve fits from the Dubinin-Astakhov equation with the experimental data for regular density silica gel, Artengel, and Art-Sorb, respectively. All three gels show some hysteresis with the desorption isotherm lying above the adsorption isotherm. Art-Sorb has the least amount of hysteresis with most of it occurring above 60%. Regular density silica gel's hysteresis occurs below 60%, while Artengel's occurs in the 30-70% range.

Figure 2. Regular density silica gel.

Figure 3. Artengel

Figure 4. Art-Sorb

Gel Comparison

In comparing the gel isotherms, it is best to focus on the 30-60% RH range since that is the desirable range for museum environments. Figure 5 shows the EMC of the three gels in the 30-60% RH range. In this range, Art-Sorb has a lower moisture capacity than Artengel and regular density silica gel, which have similar capacities.

Figure 5. Equilibrium moisture capacity of three gels in the relative humidity range of 30-60%.

In evaluating the buffering performance of the three gels, it is more appropriate to use the change in moisture capacity over a given RH range, represented by the M-value, rather than the specific moisture capacity at a specific RH as shown on the isotherm plots. Over a given RH range, a gel with a linear isotherm will have a constant M-value and thus a constant performance, while a gel with a non-linear isotherm will have a varying M-value and thus its performance will vary with RH. Since the M-value is essentially the slope of the isotherm at a given RH, it can be calculated for each of the three gels by taking the derivative of the D-A equation. Figure 6 compares the M-values for the three gels based upon their adsorption isotherms over the 30-60% RH range. Artengel has a fairly constant M-value of 7 g/kg. The M-value for Art-Sorb increases with RH from 3 to 10 g/kg, while regular density's M-value decreases with RH from 6 to 3 g/kg.

Figure 6. Comparison of M-values for the three adsorbants in the 30-60% RH range.

Based upon these results, Artengel would be expected to have a consistent performance over the 30-60% RH range. Art-Sorb's performance would be better in the higher RH range, while regular density's performance would be better in the lower RH range.

Using eq. 1, Thomson's original calculations were revisited using the present results to determine the amount of each gel required to achieve a case half-time of 150 days with a case leakage rate of 1 ACD. Table 3 lists these results along with the calculated cost of each gel per unit of case volume.

The results presented in Table 3 are based upon each gel's M-value at 45% RH (the middle of the 30-60% range). Art-Sorb's M-value was calculated using both the measured isotherm data and the data listed in the company's literature. Regular density silica gel costs are calculated from the stated bulk price from a common manufacturer. The costs for Artengel and Art-Sorb are based upon each company's stated price for bead type media.

Since Artengel has the highest M-value of 7 g/kg, it has the smallest sizing factor of 5 kg/m³. Art-Sorb and regular density silica gel have about the same M-value around 5g/kg and thus have similar sizing factors of around 7 kg/m³. On a cost basis, Artengel and regular density have nearly the same unit cost (i.e. cost per unit of case volume), while Art-Sorb has more than double the cost of regular density silica gel.

Case Model

In order to evaluate the long-term performance of the three gels under varying conditions, a computer model was developed. The following assumptions were used in the modeling of silica gel behavior inside of a display case:

• Case material and artifact have negligible water buffering capacity i.e. the buffering material preferentially adsorbs and desorbs moisture.
• No spatial variation of RH inside the display case.
• Dry bulb temperature inside the case microenvironment is the same as the building macroenvironment.
• Temperature of the buffering media is the same as the dry bulb temperature in the case microenvironment.

The two water exchange processes included in the model are: (1) the exchange of water vapor between the case microenvironment and ambient building macroenvironment air due to infiltration and (2) the exchange of water vapor between the gel and case air. The rate of water exchange due to infiltration is expressed by:

Because the movement of air inside a well-sealed display case is dominated by free convection, intra-particle resistance is assumed to be negligible and the transport of water vapor from the bulk case air to the gel surface is assumed to be the dominant resistance to mass transfer. From the work of Kafui (1994), the rate of mass transfer from the case air to the gel surface can be described by a lumped external mass transfer coefficient, Kgel, with the change in water concentration of the adsorbent media with time being expressed by:

A water balance that includes these two water exchange processes can be written

where m_H2O is the mass of water in the case at time t and m_H2O,0 is the initial mass of water. Knowing m_H2O, the relative humidity can be calculated as a function of time using psychrometric relations.

Model Validation

The validity of the model was determined by comparing model predictions with the results of a long-term experiment that measured the RH inside three moisture-impervious containers, each with a volume of 3.79 liters.

Each container held a 10-gram sample of one of the three gels which was initially conditioned to an RH of 43%. A 30-mm hole located in the top of each container allowed each container to have a similar leakage rate. The RH inside the containers and the ambient room value was measured using a Hobo H8 Pro Series Temp/RH sensor. The long-term experiments involved monitoring the RH for a period spanning 42 days.

Figure 7 compares the model predictions with the long-term experimental data for regular density silica gel. Figure 8 compares the performance of the three gels for the long-term experiment. Regular density silica gel and Artengel perform almost identically with a final RH of 26%, while Art-Sorb is less effective with a final RH of 20%. For all three gels, the model prediction is within the ±3% accuracy of the measured data.

Figure 7. Comparison of model prediction with experiment data for regular density silica gel.

Figure 8. Comparison of gel performance for long-term experiment.

Simulation of Silica Gel Performance

Using the model, simulations were run to evaluate the performance of the three gels inside display cases under varying building and case conditions. Three different ambient building RH profiles representing a dry, humid, and moderate building environments were used to drive the model. A dry building environment was simulated by using RH measurements taken over a one-year period at the Field Museum of Natural History. The 7-month heating season from October to April results in an average annual building RH of 35% with the RH dropping below 40% for 60% of the year. A humid building environment was simulated by inverting the Field Museum data to create an average annual building RH of 55%. A moderate building environment was represented by a sine wave with an average RH of 45% and an amplitude of 15%.

The three variables analyzed with the model were the case leakage rate, amount of gel inside the case, and the type of gel. For Art-Sorb, simulations were run using both the company's adsorption isotherm data and the isotherm determined from the current study's experiments. Table 4 lists the parameters and values that were used in the simulations.

Simulation Results

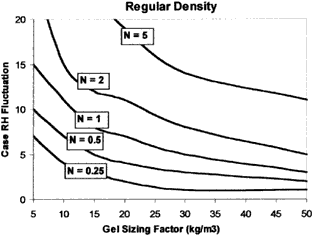
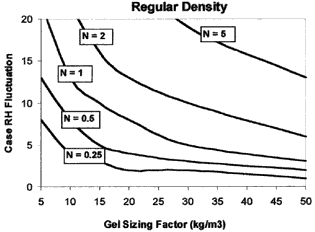
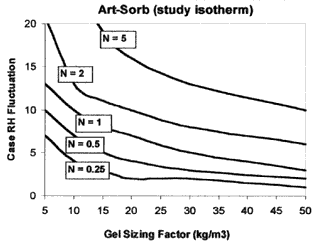
Figures 9-11 compare the simulation results for the dry, humid, and moderate building RH environments, respectively. The Y-axis on each plot is the maximum predicted RH fluctuation inside a case over a one-year simulation. The X-axis is the amount of gel inside the case per unit of case volume in the units of kg/m3. The different lines on each graph represent the performance of the gel at a specific case leakage rate value, N, in units of air changes per day. For example, looking at the Artengel plot in Fig. 9, a case with a leakage rate of 2 ACD (n=2) and containing 20 kg/m3 of gel would undergo an RH fluctuation of 8% from the desired set point of 45% over an entire year in a dry building environment.

For all three building environments, Artengel has the best performance yielding smaller case RH fluctuations than the other two gels for a given case leakage rate and gel sizing factor. Since it has a constant M-value over the 30-60% RH range, Artengel's performance is not affected by different building environments. Since its M-value increases with RH, Art-Sorb performs better in a humid building than a dry one. In contrast, regular density silica gel performs better in a dry building than a humid one because its M-value is highest in the lower RH range.

There is little difference in the predicted performance of Art-Sorb using either the company or current study's isotherm data. The amount of gel required to keep the RH fluctuation to an acceptable level increases as the case leakage rate increases. If the maximum desired case RH fluctuation over a one-year period is 10%, then a case leakage rate of 2 ACD or less is necessary. Higher case leakage rates would require more than 30 kg/m3 of gel which would likely be impractical and costly. Within the case leakage range of 0.25-2 ACD, between 5-30 kg/m3 of silica gel would be required for adequate control over a one-year period.

Figure 9. Maximum predicted case RH fluctuations over one-year simulation for three silica gels in a dry building environment for different case leakage rates (N) and gel sizing factors

Figure 10. As above, for humid building environment

Figure 11. As above, for moderate building environment

Conclusions

Based upon the experimental and computer simulation results of this study, the following conclusions can be made:

• All three gels would provide effective RH control using Thomson's recommendation of 20 kg/m3 if the case leakage rate is 1 ACD or less.
• On a pound for pound basis, Artengel has a higher buffering capacity than either regular density silica gel or Art-Sorb.
• On a cost basis, regular density silica gel and Artengel have about the same cost for a given amount of buffering capacity while Art-Sorb has twice the cost.
• Over the RH range of 30-60%, Artengel has a consistent performance, while Art-Sorb performs better above 50% and regular density silica gel performs better below 40%.
• For the conditions investigated, a case with a leakage rate of greater than 2 ACD would require more than 30 kg/m3 of gel in order to keep the display case RH fluctuation at 10% or below over a one year period.
• For the conditions investigated, a case with a leakage rate of 2 ACD or less would require 5-30 kg/m3 of gel to keep display case RH fluctuations to 10% or less over a one year period.

References

ASHRAE, Applications Handbook, American Society of Heating, Refrigerating, and Air Conditioning Engineers, Atlanta, GA (1999).

Ault, J., S.A. Klein, D.T. Reindl, J. Guay, "Indoor Environmental Control: Review of Current Recommendations and Survey of Conditions at the Chicago Field Museum," accepted for ASHRAE Transactions, March, 2001.

CCI (1984). Technical Bulletin 10: Silica Gel. CCI. Ottawa, Canada.

Dubinin, M., "Physical Adsorption of Gases and Vapors in Micropores," Prog. Surf. Membrane Science, 9, pp. 1-70, (1975).

Erhardt, D. and Mecklenburg, M., "Relative Humidity Re-examined," Preventive Conservation: Practice, Theory and Research, ed. by A. Roy and P. Smith. London, IIC, pp. 32-38, (1994).

Greenspan, L., "Humidity Fixed Points of Binary Saturated Aqueous Solutions," Journal of Research of the National Bureau of Standards - A. Physics and Chemistry, Vol. 81A, No. 1, Jan-Feb, (1977).

Guinchen, G., and Gai, V., "Controle du climate autour de 197 instruments de musique," 7th Triennial Meeting, ICOM Committee for Conservation, Copenhagen, 84.17.19-84.17.25, (1984).

Kafui, K.D., "Transient Heat and Moisture Transfer in Thin Silica Gel Beds," Transactions of the ASME, Vol. 116, pp. 946-953, Nov., (1994).

Polanyi, M., "Theory of Adsorption of Gases. A General Survey and some Additional Remarks," Trans. Far. Soc., Vol. 28, 316-333, (1932).

Schweizer, F., "Stabilization of RH in Exhibition Cases: An Experimental Approach," 7th Triennial Meeting, ICOM Committee for Conservation, Copenhagen, 84.17.50-84.17.53, (1984).

Stolow, Nathan, "The Microclimate: A Localized Solution," Museum News, Vol. 56(2): pp. 52-63, (1977).

Thomson, G., "Stabilization of RH in Exhibition Cases: Hygrometric Half-time," Studies in Conservation, Vol. 22, pp. 85-102, (1977).