3 THEORY

Hendriks's model is based on the presence of oxidant and reducing gases in the environment surrounding the photograph. We will therefore explore the possibility that the occurrence of the silver-mirroring edge pattern is related to the diffusion and reaction of environmental gases with the photograph. The silver-mirroring pattern will in general result from competition between reactions, consuming the gases at the emulsion surface, and diffusion in air, transporting the gases toward the plate surface. To compare model predictions concerning the shape and extent of silver-mirroring edge patterns with actually observed edge patterns, both processes have to be included in a single model.

Modeling of the reaction between the plates and the gas in terms of a reaction-rate law is, in principle, complicated. Indeed, the reaction process depends on many parameters: the amount and nature of the gases (e.g., strong or weak oxidants), the amount and nature of the silver compounds in the emulsion (e.g., metallic silver or silver salts), the state of the silver e.g., filamentary or colloidal silver), and the potential shielding of surface emulsion layers against gas penetration (e.g., the silver mirroring layer itself). As no detailed information on these rates is currently available, we can merely attempt to calculate the effects for some simple reaction-rate laws and compare the results with observations.

Modeling of the gas diffusion process toward the plate is relatively straightforward. The gas diffusion to the plates is determined by the geometry of the plate in the space, which is the position and shape of the plate, by the diffusion coefficient in air for the specific type of gas, and by the presence of ventilation that gives rise to convection currents able to alter the simple gas diffusion.

The full general equations describing this phenomenon of diffusion and reaction are complicated to solve. We will restrict our discussion to a few simple cases starting from simplifying assumptions in terms of both geometry and reaction-rate laws.

We will discuss two different geometries under which a plate can be exposed to reactive gases: (1) plates kept in stacks and (2) plates freely exposed to the environment.

3.1 STACKED-PLATE EXPOSURE

Let us consider silver gelatin glass plates kept in a stack, as, for example, the glass plates contained in a traditional box. The gases will penetrate from the surrounding air to the space between the plates, where they will be consumed by the reaction with the silver in the emulsion layers. The silver-mirroring pattern will also, in this case, be determined by the rate of diffusion of the gas parallel to the plate surface and by the rate of reaction with the plates. The amount of gas diffusing parallel to the plates will be proportional to the distance between the plates: the higher the distance, the higher the amount of gas able to diffuse between the plates. If the reactivity is high, the gas will be consumed as soon as it penetrates between the plates, and the silver mirroring will be confined to the very edge of the plate. If, on the other hand, the reactivity is low, the diffusion term will prevail over the reaction term, and the silver mirroring will be spread all over the plate.

The simplest mathematical model that can predict an edge pattern assumes that the glass plate surfaces are parallel to each other and that the amount of gas reacting with the plates is proportional to the gas concentration at the plate surface, the constant of proportionality being the reaction probability (see appendix 1 for details). The gas absorption rate Ψ (g cm-2 s-1) decreases exponentially with the distance x (cm) from the plate edge according to:

Equation (3.1).

The extension δ (cm) of silver mirroring can be taken as the distance at which the initial value of Ψ has halved:

Equation (3.2).

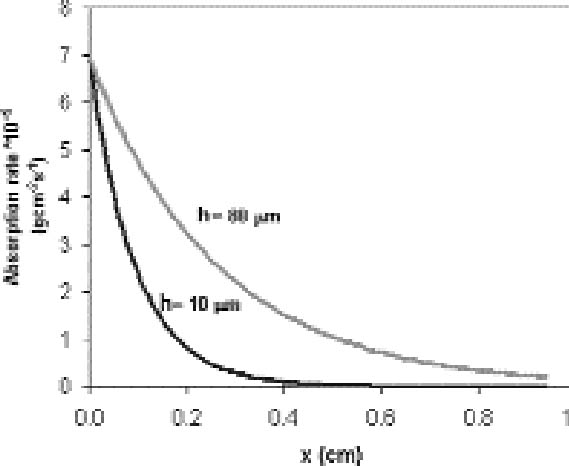
For a single plate we assume the reaction probability for the whole surface to be constant. From equation (3.2), it is then expected that the extension of silver mirroring is proportional to the square root of the distance between the plates. Figure 6 shows the decay of the silver mirroring for two different distances. The increase in the silver-mirroring extension with distance suggests that local variations of the silver-mirroring extension on a plate, like the ones in figure 4, could depend on local variations of the distance between two adjacent plates of the stack, taking place, for example, if the plates are buckled and not flat. Indeed, glass plates from before 1940 are not completely flat (Koob 2000). Although equations (3.1) and (3.2) have been developed for parallel plates with a single uniform distance, the equations will also apply to the case of slightly curved plates. As long as the distance variation is small within the typical width of the silver-mirroring pattern, the plates can still be considered as being locally parallel.

Fig. 6.

Decay of the gas absorption rate with penetration distance for parallel plates kept at two different distances. The smaller the distance between the plates, the faster the decay and hence the smaller the predicted silver-mirroring extension.

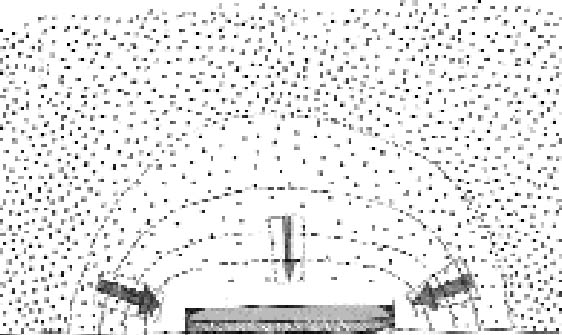
If, on the other hand, we fix the distance between the plates, the extension of silver mirroring will be inversely proportional to the square root of the reaction probability. High reaction probabilities will give rise to narrow and sharp silver mirroring patterns.

It is important to stress that an exponential decrease in the silver-mirroring intensity with the distance from the edge is a direct consequence of the assumption that the amount of gas reacting is proportional to the gas concentration. Other types of reaction kinetics (e.g., reactions dependent on some power of the gas concentration or on the amount of silver available in the emulsion) would result in other than exponential distribution profiles of the silver-mirroring intensity.

3.2 SINGLE-PLATE EXPOSURE

Consider a single silver gelatin glass plate freely exposed to a surrounding atmosphere containing a reactive gas. Because the gas reacts with the silver contained in the glass plate emulsion, the gas concentration in the proximity of the plate surface will be lower than the gas environmental concentration. The resulting difference in gas concentration between the environment and the space adjacent to the plate drives a constant flow of gas from the environment to the plate. The areas on the plate where the gas flow is higher will have a stronger silver mirroring. Two extreme cases can be considered.

If the reactivity of the gas with the emulsion is low, there will be hardly any flow of gas from the environment to the plate. As a result, the gas concentration at the entire plate surface will be close to the environmental concentration, and the distribution of silver mirroring on the plate will be homogeneous. The same result will be achieved when the reactivity is high but external ventilation forces the gas concentration to be evenly distributed around the plate.

If the reactivity is high and there is no ventilation, then the gas concentration near the plate will be practically zero, since every gas molecule reaching the plate will be immediately consumed by the reaction. In this case, we can qualitatively predict the distribution of the gas flow on the plate by looking at the shape of the planes of equal gas concentration, which are imaginary planes connecting points in the space having the same concentration value (fig. 7). The shape of the planes of equal concentration will resemble the plate in its proximity and, for symmetry reasons, will be spherical at a certain distance. As illustrated in figure 7, the gas concentration difference is steeper at the plate edges, and consequently the gas flow on the plate will be higher at the edges than at the center. A silver-mirroring edge pattern will arise.

Fig. 7.

Planes of equal gas concentration surrounding a plate freely exposed to environmental gases without ventilation. As the planes are closer at the plate corners, the flow of gas is higher at the plate corners than at the center, and a silver-mirroring edge pattern arises.

We have calculated with a mathematical model based on the assumptions of no ventilation and high reactivity (see appendix 2 for details) the amount of gas reacting per unit surface and time with the plate, the so-called gas absorption rate. In an initial approximation, the gas absorption rate can be assumed to be proportional to the visual intensity of silver mirroring. Figure 8a shows the calculated pattern for a hypothetical circular plate, while figure 8b shows the pattern for a rectangular plate.

In the case of both the circular and the rectangular plate, the model predicts a higher absorption rate at the edges of the plate than at the center.