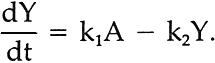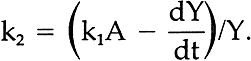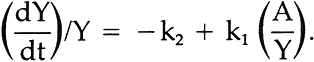DETERMINATION OF THE SPECIFIC RATE CONSTANT FOR THE LOSS OF A YELLOW INTERMEDIATE DURING THE FADING OF ALIZARIN LAKE
Robert L. Feller, Ruth M. Johnston-Feller, & Catherine Bailie
4 EQUATIONS FOR THE RATE OF FORMATION AND LOSS OF THE INTERMEDIATE
IN VIEW OFEQUATION iii, the concentration of intermediate Y at any time, t, can be accounted for by the following equation:
Fig. .
 |
This equation states that the observed change in the amount of Y at any time (dY/dt) is equal to the opposite from the rate of loss of A (this is because Y is produced from A; hence dY/dt = dA/dt in step k1) minus the rate of disappearance of Y in step k2, which we have here assumed also to follow a decay law such as expressed for component A in equation i. Taking into consideration i, this equation may be written:
Fig. .
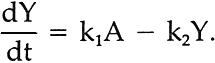 |
Dividing by Y and rearranging, the equation yields an expression for k2:
Fig. .
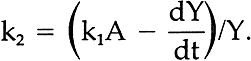 |
We chose to obtain k2 by rearranging vi further to conform to the general equation for a straight line, y = b + mx, where m is the slope and b is the intercept on the y ordinate. Thus:
Fig. .
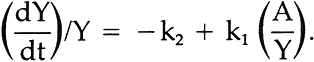 |
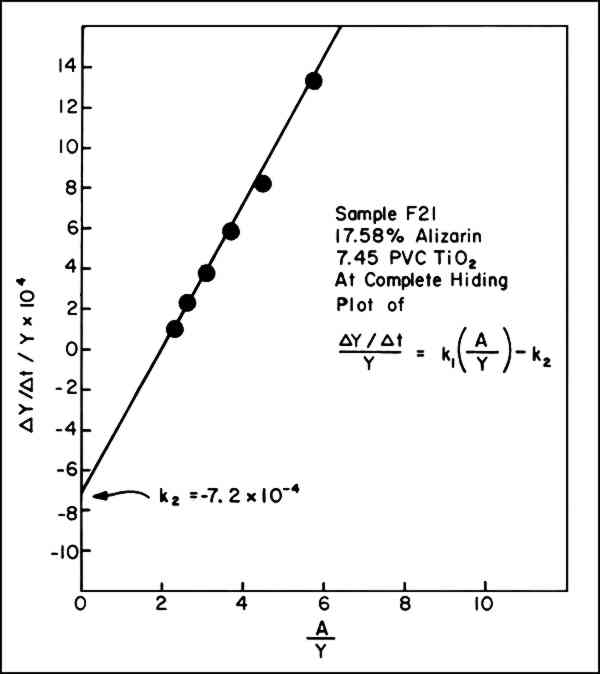
Thus, if equation iii indeed represents the sequence of chemical steps involved, each of which proceeds by first-order kinetics, a graph of the values of (dY/dt)/Y versus A/Y should yield a straight line with the slope equal to k1 and the intercept, k2. A typical graph is shown in Figure 2
Fig. 2.
Graphical solution of equation vii, (dY/dt)/Y on y axis versus A/Y on x axis. Data taken from Table I and Figure 3.
 |
|