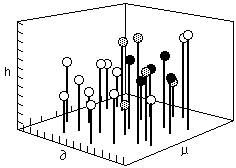
Fig. 3 A three dimensional box used to plot solubility information after Crowley, Teague and Lowe) = Hildebrand value, µ = dipole moment, h=hydrogen bonding value
Solubility Parameters: Theory and Application
John BurkeSolubility behavior can be adequately described using Hildebrand values, although in some cases differences in polar composition give unexpected results (Fig. 1, for example). Predictions become more consistent if the Hildebrand value is combined with a polar value (i.e. hydrogen bonding number), giving two parameters for each liquid. Even greater accuracy is possible if all three polar forces (hydrogen bonding, polar forces, and dispersion forces) are considered at the same time. This approach assigns three values to each liquid and predicts miscibility if all three values are similar.
As long as data is presented in the form of a single list, or even a two dimensional graph, it can be easily understood and applied. With the addition of a third term, however, problems arise in representing and using the information; the manipulation of three separate values presents certain inconveniences in practical application. It is for this reason that the development and the use of three component parameter systems has centered on solubility maps and models.
While polymer solubilities may be easily presented as a connected group of solvents on a list, or as a specific area on a graph, the description of solubilities in three dimensions is understandably more difficult. Most researchers have therefore relied on three-dimensional constructions within which all three component parameters could be represented at once.
In 1966, Crowley, Teague, and Lowe of Eastman Chemical developed the first three component system using the Hildebrand parameter, a hydrogen bonding number, and the dipole moment as the three components. A scale representing each of these three values is assigned to a separate edge of a large empty cube. In this way, any point within the cube represents the intersection of three specific values. A small ball, supported on a rod, is placed at the intersection of values for each individual solvent (Figure 3).
Fig. 3 A three dimensional box used to plot solubility
information after Crowley, Teague and Lowe) = Hildebrand value,
µ = dipole moment, h=hydrogen bonding value
Once all the solvent positions have been located within the cube in this way, solubility tests are performed on individual polymers. The position of solvents that dissolve a polymer are indicated by a black ball, nonsolvents by a white one, and partial solubilities are indicated by a grey ball. In this way a solid volume (or three dimensional area) of solubility is formed, with liquids within the volume being active solvents (black balls), and liquids outside the volume being non-solvents (white balls). Around the surface of the volume, at the interface between the area of solubility and the surrounding non-solvent area, the balls are grey.
Once the volume of solubility for a polymer is established, it becomes necessary to translate that information into a form that is practical. This means transforming the 3-D model (difficult to carry around) into a 2-D graph (easier to publish). This is usually done in one of two similar ways. In both cases, the data is plotted on a rectangular graph that represents only two of the three component parameter scales (one side of the cube).
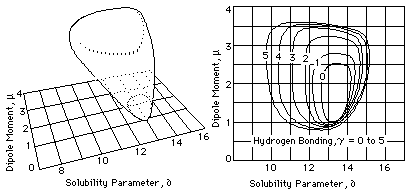
Fig. 4 Approximate Representations of Solid Model and
Solubility Map for Cellulose Acetate (from Crowley, et al,
Journal of Paint Technology Vol 39 # 504, Jan 1967)
The polymer solubility volume takes the form of an area on the graph that represents either a single slice through the volume at a specified value on the third component parameter scale, or a topographic map that indicates several values of the third parameter at the same time (see Figure 4). Because the volume of solubility for a polymer usually has an unusual shape, several graphs are often needed for an individual polymer if its total solubility behavior is to be shown.
Maps such as these can be used in conjunction with a table of three component parameters for individual solvents, and in this way provide useable information about solvent-polymer interactions and allow the formulation of polymer or solvent blends to suit specific applications. Data presented in this way is not only concise, but saves considerable time by allowing the prediction of solubility behavior without recourse to extensive empirical testing. It is for these reasons that solubility maps are often included in technical reports and manufacturer's product data sheets. How graphs are actually used to accomplish these purposes will be described later in terms of the triangular Teas graph, in which these procedures are similar but greatly simplified.
The most widely accepted three component system to date is the three parameter system developed by Charles M. Hansen in 1966. Hansen parameters divide the total Hildebrand value into three parts: a dispersion force component, a hydrogen bonding component, and a polar component. This approach differs from Crowley's in two major ways: first, by using a dispersion force component instead of the Hildebrand value as the third parameter, and second, by relating the values of all three components to the total Hildebrand value. This means that Hansen parameters are additive:
t2 =
(6) where
The numerical values for the component parameters are determined
in the following way: First, the dispersion force for a particular
liquid is calculated using what is called the homomorph
method. The homomorph of a polar molecule is the nonpolar molecule
most closely resembling it in size and structure (n-butane is the
homomorph of n-butyl alcohol). The Hildebrand value for the
nonpolar homomorph (being due entirely to dispersion forces) is
assigned to the polar molecule as its dispersion component value.
This dispersion value (squared) is then subtracted from the
Hildebrand value (squared) of the liquid, the remainder designated
as a value representing the total polar interaction of the molecule
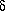a (not to be confused with the polar
component 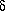p). Through trial and error experimentation
on numerous solvents and polymers, Hansen separated the polar value
into polar and hydrogen bonding component parameters best reflecting
empirical evidence. Table 3 lists Hansen parameters for several
solvents.
Sorry, as of 2/5/96, [TABLE 3] is not yet available
Charles Hansen also used a three-dimensional model (similar to
that used by Crowley et al.) to plot polymer solubilities. He found
that, by doubling the dispersion parameter axis, an approximately
spherical volume of solubility would be formed for each polymer.
This volume, being spherical, can be described in a simple way
(Figure 5): the coördinates at the center of the solubility
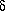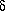sphere are located by means of three component parameters (d, p, 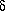h), and the radius of the sphere is
indicated, called the interaction radius (R). Table 4 gives
the Hansen parameters and interaction radius of several
polymers.
Fig. 5
The Hansen volume of solubility for a polymer is located within a
3-D model by giving the coördinates of the center of a
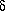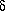solubility sphere ( d, p,
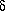h) and its radius of interaction (R).
Liquids whose parameters lie within the volume are active solvents
for that polymer.
| /MPa1/2 |
||||
| Polymer (trade name, supplier) | d |
p |
h |
R |
|---|---|---|---|---|
| Cellulose acetate (Cellidore® A, Bayer) | 18.6 | 12.7 | 11.0 | 7.6 |
| Chlorinated polypropylene (Parlon® P-10,Hercules) | 20.3 | 6.3 | 5.4 | 10.6 |
| Epoxy (Epikote® 1001,Shell) | 20.4 | 12.0 | 11.5 | 12.7 |
| Isoprene elastomer (Ceriflex®IR305, Shell) | 16.6 | 1.4 | -0.8 | 9.6 |
| Cellulose nitrate (1/2 sec,H-23, Hagedorn) | 15.4 | 14.7 | 8.8 | 11.5 |
| Polyamide, thermoplastic(Versamid® 930, General Mills) | 17.4 | -1.9 | 14.9 | 9.6 |
| Poly(isobutylene)Lutonal® IC-123, BASF) | 14.5 | 2.5 | 4.7 | 12.7 |
| Poly(ethylmethacrylate) (Lucite® 2042, DuPont) | 17.6 | 9.7 | 4.0 | 10.6 |
| Poly(methyl methacrylate) (Rohm and Haas) | 18.6 | 10.5 | 7.5 | 8.6 |
| Polystyrene (Polystyrene LG, BASF) | 21.3 | 5.8 | 4.3 | 12.7 |
| Poly(vinyl acetate) (Mowilith® 50, Hoechst) | 20.9 | 11.3 | 9.6 | 13.7 |
| Poly(vinyl butyral) (Butvar®B-76, Shawnigan) | 18.6 | 4.4 | 13.0 | 10.6 |
| Poly(vinyl chloride)(Vilpa® KR, k=50, Montecatini) | 18.2 | 7.5 | 8.3 | 3.5 |
| Saturated polyester (Desmophen® 850, Bayer) | 21.5 | 14.9 | 12.3 | 16.8 |
A polymer is probably soluble in a solvent (or solvent blend) if the Hansen parameters for the solvent lie within the solubility sphere for the polymer. In order to determine this (without building a model) it must be calculated whether the distance of the solvent from the center of the polymer solubility sphere is less than the radius of interaction for the polymer:
D(S-P) = [4( (7) where
D(S-P) = Distance between solvent and center of solubility sphere
(The figure "4" in the first term of equation (7), which doubles the dispersion component scale, is intended to create a spherical volume of solubility.) If the distance ( D(S-P) ) is less than the radius of interaction for the polymer, the solvent would be expected to dissolve the polymer. This method avoids the reliance on graphic plots of solubility behavior and can be used effectively in solely numerical form. The mathematics involved are inconvenient however (especially when solvent blends are concerned), and it is perhaps for this reason that the use of this excellent system is not more widespread.
Hansen parameters are both reasonably accurate in predicting solubility behavior and concise in their representation of that information. Accurate because precise values for all three component parameters are utilized, and concise because the entire solubility volume for a polymer can be numerically indicated by four terms: one set of parameters and a radius.
On the other hand, a two-dimensional graph sacrifices some of that accuracy and conciseness in return for a system that clearly illustrates the relative positions of numerous materials, and can be easily used in practical applications. Predicting whether a polymer is soluble in a mixture of two solvents, for example, while possible mathematically, is accomplished on a graph by drawing a line between the two solvents and seeing whether that line passes through the area of solubility for the polymer.
As was the case with Crowley's solubility maps, Hansen's three dimensional volumes can be similarly illustrated in two dimensions by plotting a cross-section through the center of the solubility sphere on a graph that uses only two of the three parameters, most commonly p and h. Figures 6 and 7 illustrate this approach by plotting the volumes of solubility for five polymers: polyvinyl acetate, polyvinyl butyral, polyvinyl chloride, polymethyl methacrylate, and polyethyl methacrylate. The graphs use the hydrogen bonding component parameter and the polar component parameter as the X and Y axis, respectively, and plot the circle generated by the radius of interaction for each polymer; the symbols indicate the respective locations of solvents.
Hansen graphs are easy to use because solvent positions are constant and polymer solubility areas may be drawn with a compass; furthermore, solvent blending calculations can be done with a pencil and ruler. The accuracy of predicting solubility behavior is about 90%, with solvent locations nearest the edge of a solubility area being the least predictable. This is due to the three-dimensional nature of the actual solubility sphere. When reduced to two dimensions, solvents that appear near the edge inside the solubility area may in fact be outside it, in front or behind, in three dimensions.
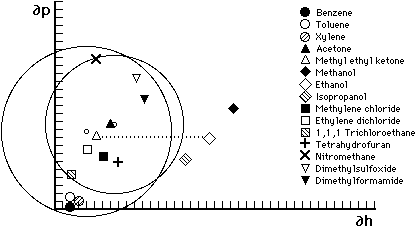
Figure 6
Hansen graph of solubility areas for polymethyl methacrylate
(smaller circle) and polyethyl methacrylate (larger circle). Liquids
parameters are indicated by symbols; small circles indicate center
of solubility spheres. Liquids outside the polymer area of
solubility are non-solvents. The dotted line illustrates all the
possible possible mixtures of MEK and ethanol--notice that MMA will
tolerate a greater proportion of ethanol than will EMA. Accordingly,
MMA should be soluble in toluene/acetone 3:1 but not in 100%
toluene.
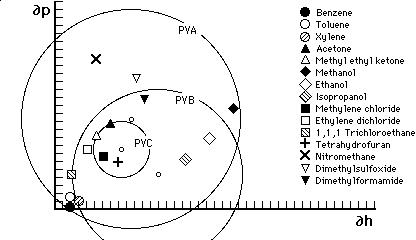
Figure 7
Hansen graph of solubility areas for polyvinyl acetate (PVA), poly
vinyl butyral (PVB) and poly vinyl chloride (PVC). This type of
graph uses only two of the three Hansen parameters
Next: Part 7 - Fractional Parameters
![[CoOL]](/icons/sm_cool.gif){kind=icon}