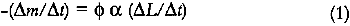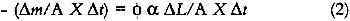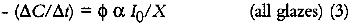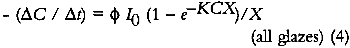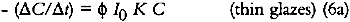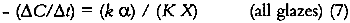APPENDIX

1 APPENDIX 1

1.1 MODEL FOR THE FADING OF TRANSPARENT GLAZES

In developing the general kinetic law for the fading of a transparent glaze, we adopt the approach of Malac (1989), in which the rate of total colorant loss is determined by the total amount of photochemically active light absorbed. This model rests on a number of simplifying assumptions, and later we discuss the extension of these kinetics to more general systems. We begin by assuming:

1. The glaze is purely absorbing, that is, there is no optical scattering.
2. The light incident upon the glaze is collimated and monochromatic.
3. The fading reaction creates nonabsorbing, nonscattering products.
4. The photochemical reaction rate depends on the amount of light absorbed.

The loss of colorant per unit time is equal to the light flux (in moles of photons per unit time) incident on the colorant, multiplied by the probability that the light is absorbed by the glaze, multiplied by the probability that an absorbed photon causes conversion of the colorant to colorless product. In symbolic notation, this is written as:

Fig. .

Fig. .

Fig. .

This expression indicates that the loss of colorant concentration will generally be proportional to the fraction of incident light absorbed by the film (represented by α). This relationship suggests two results: The concentration loss rate in very highly absorbing glazes will be constant as long as the absorption strength does not change during the fading; and the loss rate will become progressively smaller as the fading proceeds and the light absorption by the glaze decreases. A more explicit analysis of these cases reveals the relationship between the fading for these extreme cases.

For transparent glazes illuminated with collimated light making a single pass through the film, the absorbed fraction of light can be expressed using Beer's law: α = 1 − e−KCX where K is the molar absorption coefficient. So the kinetic relation (3) becomes:

Fig. .

For very highly absorbing glazes (optically thick), all of the incident light is absorbed by the glaze (α = 1, or alternatively KCX is very large and e−KCX = 0), and a small concentration loss does not appreciably alter the amount of light that is absorbed. The kinetic expression for the overall concentration loss becomes:

Fig. .

Fig. .

In these glazes, the upper layers of colorant completely absorb the photochemically active wavelengths and fade while effectively protecting the underlying strata. This process has been observed in dye fading in films and textiles and has been dubbed the “layer effect” or the “filter effect.” Giles has reviewed the major observations and descriptions of this phenomenon in dye studies (Giles and Forrester 1980), and this same behavior has been alluded to in the analysis of the fading of very highly absorbing glazes by Johnston-Feller (1986).

For glazes that absorb only a fraction of the photochemically active wavelengths of incident light, the exponential term in equation 4 can be approximated e−KCX ≅ 1−KCX), and the kinetic relation becomes:

Fig. .

This approximation for the exponential term is reasonable for KCX < 0.3, that is, for glazes having transmittances above about 75%.

Equation 6a describes a rate of colorant loss that is proportional to colorant concentration: each increment of fading will cause the glaze to absorb slightly less light, causing the subsequent reaction to occur more slowly. This is an example of a so-called “first-order” reaction, and for such a process the concentration decreases exponentially with time:

Fig. .

It is valuable to examine the relationship between the zero-order rate constant of the “thick” glaze fading and the first-order rate constant of the “thin” glaze fading. One can see that the zero-order rate constant (i.e., the slope of the linear fading of the thick glaze) is equal to the first-order reaction rate constant divided by K X (the product of absorption coefficient and film thickness). Thus one can recast the general kinetic expression of equation 3 in terms of this first-order reaction rate constant:

Fig. .

At this point, it is appropriate to examine the validity of the original simplifying assumptions that were the basis for this description. The most obvious restriction of the model is its presumption of monochromatic illumination that allows the use of absorption coefficients and quantum yields of reaction for a single wavelength. Strictly speaking, the model can be extended to describe fading due to polychromatic illumination (far more typical of gallery lighting) by summing the effects of each wavelength (that is, the appropriate absorption coefficients and quantum yields) across the spectrum. This approach is similar to that used by Krochmann (1988) and necessitates the measurement of reaction rates due to absorptions at different wavelengths. It seems likely, however, that this fineness of detail may be unnecessary for describing fading due to absorption in a single broad spectral peak, which probably can be adequately described according to an average quantum yield for reaction due to absorption in that peak. As long as the description is thus restricted to illumination with a visible light source, so that the fading due to visible and ultraviolet wavelengths need not be summed, the above treatment should be adequate if the average values of absorption and reaction probabilities are used. Another assumption in this model is that the absorbed wavelengths are also the photochemically active ones. Recent studies have tended to support the notion that, provided that only a single absorption band is present, the absorption spectrum for the colorant coincides with the action spectrum of wavelengths that produce most of the photochemical reaction (McLaren 1956; Saunders and Kirby 1994).

The assumption of collimated light incident on the glaze film is also an inaccurate representation of the combination of diffuse and oblique collimated light often used to illuminate objects. Similarly, glazes are usually viewed over a reflective and optically scattering substrate, and the light fluxes within the film are expected to more closely approximate diffuse fluxes than collimated ones. It has been pointed out by many authors that the absorption coefficient of diffuse light is about twice that of collimated fluxes, probably by virtue of the greater absorption path length for the light traveling at oblique angles in the film (Beasley et al. 1967). As a result, the kinetic behavior for fading of glazes illuminated by diffuse light should be the same as for collimated light, with the absorption coefficients doubled. Also, since the model assumes that the light intensity distribution has no effect on the rate for the total colorant loss, the model should adequately describe fading of a glaze on a reflective substrate. For these reasons, the simple model that has been described is expected to allow at least qualitative predictions of the course of fading of a glaze under any given illumination and also to allow semiquantitative comparison of different glaze formulations when exposed to the same illumination.

2 APPENDIX 2: EXPERIMENT

Glazes of known pigment loadings were prepared by first ball milling for 3.5 days dry Pigment Red 66 (Colour Index No. 18000:1, a barium salt of an azo dye) in a xylene/toluene solution of poly(vinyl acetate) (PVA). The proportions of pigment, resin, xylene and toluene in this base paint were 2.83:37.04:47.10:13.00 by weight. This pigment dispersion was mixed in varying proportions with a 44% by weight solution of PVA in xylene in order to produce transparent paints of the desired pigment concentrations. Two paints were prepared: one, used to make glaze 5 and the thin glazes in figure 5, produced dry films at a pigment volume concentration (PVC) of 1.14% (2.24% pigment by weight of dry film), and the other, used for glazes 1-4, produced films having 0.68% PVC (1.34% pigment by weight). These transparent red paints were applied to 2.5 � 7.6 cm glass microscopes slides that had been precoated with layers of titanium white paint (in PVA) at complete hiding. The red paints were drawn down using a doctor blade on the white substrates at varying thicknesses to achieve the desired depth of shade for the glazes.

The glazes were exposed in a commercial fading apparatus that employs a xenon light source, filtered to eliminate infrared and short ultraviolet wavelengths, and a parabolic reflector. Collimated light was directed onto a water-cooled sample tray held at 20�C with a recirculating water chiller. An additional filter consisting of a 3.2 mm thick sheet of ultraviolet-absorbing Plexiglas (UF-3) was placed just above the samples so that only visible wavelengths were incident upon them. Visible light intensity during the exposures was 12,600 footcandles (1.36 � 105 lux), and ultraviolet light intensity (between 300–400 nm wavelength) was 1.56 � 10−4 watts/cm2, as measured at the sample position with a radiometer.

Reflectance spectra of the glazes were measured periodically during the exposures using a spectrophotometer. Measurements at 20 nm wavelength intervals were made both with the specular reflection included (for chemical kinetic analysis) and excluded (for color analysis). From these experimental data and from the model reflectance spectra of ideal red glazes, tristimulus values (X,Y,Z) were calculated for CIE standard illuminant C using the standard formulas and tables. These values were in turn used to calculate Munsell notations (hue, value, chroma), chromaticity coordinates (x, y), and color differences ΔE (CIE 1976 L∗a∗b∗ equation) using either commercial color-analysis software or a Microsoft Excel spreadsheet. Photochemical reaction kinetics were studied by calculating the absorbances (proportional to the pigment concentrations) using Beer's law, Abs = −0.5 ln (Rinternal), where ln represents the natural logarithm. In this relation Rinternal is the so-called internal reflectance, which is calculated from the total reflectance (specular reflection included) using the appropriate equation (Johnston-Feller and Bailie 1982).

ACKNOWLEDGEMENTS

This work was performed at the Research Center on the Materials of the Artist and Conservator at Carnegie Mellon University and was supported by a grant from the Andrew W. Mellon Foundation. The authors also thank R. Roberts of Sandoz Chemicals Corp. (now Clariant Corp.) for kindly supplying the Pigment Red 66 and Hugh Davidson of Davidson Colleagues for the color-analysis computer software.

REFERENCES

Barker, S. G., H. R.Hirst, and P. N.Lambert.1927. Relation between initial depth of shade and loss of colour due to fading. Journal of the Society of Dyers and Colourists43: 264–66.

Beasley, J. K., J. T.Atkins, and F. W.Billmeyer. 1967. Scattering and absorption of light in turbid media. In Electromagnetic scattering, ed.R. L.Rowell and R. S.Stein. New York: Gordon and Breach Science Publishers. 765–85.

Calvert, J. G. and J. N.PittsJr.1966. Photochemistry. New York: John Wiley and Sons.

Clough, R. L., K. T.Gillen, and C. AQuintana. 1985. Heterogeneous oxidative degradation in irradiated polymers. Journal of Polymer Science: Polymer Chemistry Edition23: 359–77.

Cunliffe, P. W., and P. N.Lambert. 1932. The measurement of the colour of dyed textiles IX: The influence of the concentration of dyestuff and the time of exposure on fading. Journal of the Society of Dyers and Colourists48: 59–66.

Feller, R. L.1975. Studies on photochemical deterioration. In ICOM Committee for Conservation Preprints, 4th Triennial Meeting, Venice. Paris: ICOM. 75/19/4/1–8.

Feller, R. L.1978. Further studies on the international blue-wool standards for exposure to light. In ICOM Committee for Conservation Preprints. 5th Triennial Meeting, Zagreb. Paris: ICOM:. 78/18/2/1–10.

Feller, R. L., and R. M.Johnston-Feller. 1981. Continued investigations involving the ISO blue-wool standards of exposure. In ICOM Committee for Conservation Preprints. 6th Triennial Meeting, Ottawa. Paris: ICOM: 81/18/1/1–7.

Feller, R. L., R. M.Johnston-Feller, and C.Bailie. 1986. Determination of the specific rate constant for the loss of a yellow intermediate during the fading of alizarin lake. Journal of the American Institute for Conservation25: 65–72.

Giles, C. H., and S. D.Forrester. 1980. Physical factors affecting the light stability of dyed and pigmented polymers. In Photochemistry of dyed and pigmented polymers, ed.N. S.Allen and J. F.McKellar. London: Applied Science Publishers. 51–91.

Gutierrez, A. R., and R. J.Cox. 1986. Maximizing light absorption at the bottom of a film. Polymer Photochemistry7: 517–21.

Johnston-Feller, R. M.1986. Reflections on the phenomenon of fading. Journal of Coatings Technology58(736): 32–50.

Johnston-Feller, R. M., and C. W.Bailie. 1982. An analysis of the optics of paint glazes: Fading. In Science and technology in the service of conservation, ed.N. S.Brommelle and G.Thomson. London: International Institute for Conservation of Historic and Artistic Works. 180–85.

Johnston-Feller, R. M., R. L.Feller, C. W.Bailie, and M.Curran. 1984. The kinetics of fading: Opaque paint films pigmented with alizarin lake and titanium dioxide. Journal of the American Institute for Conservation23: 114–29.

Judd, D. B., and G.Wyszecki. 1975. Color in business, science and industry. 3d ed.New York: John Wiley and Sons.

Krochmann, J.1988. Illumination of light-sensitive display pieces with special consideration to their damage by optical radiation. Restauro3: 227–34.

Malac, J.1989. Photochemistry in well-mixed and in stationary layers: Case 1. Polymer Degradation and Stability26: 57–63.

McLaren, K.1956. The spectral regions of daylight which cause fading. Journal of the Society of Dyers and Colourists72: 86–99.

Morton, T. H.1949. The practical assessment of the light fastness of dyeings. Journal of the Society of Dyers and Colourists65: 597–605.

Reiser, A., and E., Pitts. 1976. Characteristic curve of crosslinking photoresists. Photographic Science and Engineering20: 225–29.

Saunders, D., and J.Kirby. 1994. Wavelength-dependent fading of artists' pigments. In Preventive conservation: Practice, theory, and research, ed.A.Roy and P.Smith. London: International Institute for Conservation of Historic and Artistic Works. 190–94.

Stearns, E. I.1969. The practice of absorption spectrophotometry. New York: John Wiley and Sons.

Thommes, G. A., and V. J.Webers. 1985. Spectral response of photosensitive systems. Part 1, General effect of radiation attenuation throughout coating thickness. Journal of Imaging Science29: 112–16.

Thomson, G.1965. Topics in the conservation chemistry of surfaces. In Application of science in the examination of works of art. Boston: Museum of Fine Arts. 78–85.

Thomson, G.1978. The museum environment. London: Butterworths.

FURTHER READING

Billmeyer, F. W., and M.Saltzman. 1981. Principles of color technology. 2d ed.New York: John Wiley and Sons.

SOURCES OF MATERIALS

Davidson Colleagues, P. O. Box 490, Tatamy, Pa. 18085

Sandoz Chemicals Corp. (now Clariant Corp.), 4000 Monroe Rd., Charlotte, N.C. 28205

Atlas Electric Devices Co., 4114 North Ravenswood Ave., Chicago, Ill. 60613

Air Products and Chemicals, Inc., 7201 Hamilton Blvd., Allentown, Pa. 18195

International Light, 17 Graf Rd., Newburyport, Mass. 01950

Neslab Instruments, Inc., P. O. Box 1178, Portsmouth, NH 03802

Macbeth Division, Kollmorgen Instruments Corp., 405 Little Britain Rd., New Windsor, N.Y. 12553

Du Pont Co., White Pigment and Mineral Products, 1007 Market St., Wilmington, Del. 19898

TALAS, 213 W. 35th St., New York, N.Y. 10001

AUTHOR INFORMATION

PAUL WHITMORE received a Ph.D. in physical chemistry from the University of California at Berkeley. Following an appointment at the Environmental Quality Laboratory at Caltech studying the effects of photochemical smog on works of art, he joined the staff at the Center for Conservation and Technical Studies at the Harvard University Art Museums. Since 1988 he has been director of the Research Center on the Materials of the Artist and Conservator at Carnegie Mellon Research Institute, where his research has been directed toward the study of the permanence of modern art and library materials. Address: Carnegie Mellon University, 4400 Fifth Ave., Pittsburgh, Pa. 15213.

CATHERINE BAILIE has an A.B. in chemistry from Bryn Mawr College. Since 1977 she has been at the Research Center on the Materials of the Artist and Conservator, where she is now an associate staff scientist. Address as for Whitmore.