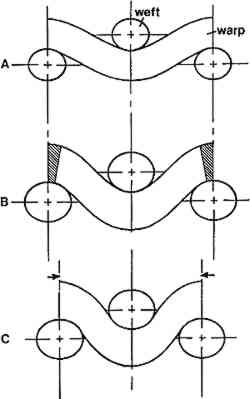
3 FABRIC SHRINKAGE IN HIGH MOISTURE LEVELS

It is well known that certain fabric supports, especially tightly woven ones, are susceptible to shrinkage at high moisture levels. An inherent characteristic of cellulosic fabrics, notably those produced since the mid-19th century, is their shrinkage response to wetting. In conservation these canvas supports are often termed “shrinkers.” While conservators have learned empirically to be wary of this type of canvas when undertaking moisture treatments, the mechanism that causes a canvas to shrink in high moisture levels is generally not well understood.Like all organic materials, the cellulosic fibers in linen and cotton fabrics swell as they absorb moisture. This swelling leads to an increase in the diameter of the yarns that make up the fabric. But surprisingly, as the yarns expand at high moisture levels, the canvas itself shrinks. To understand this phenomenon, the mechanisms of this process need to be examined in some detail.

The fundamental mechanisms of fabric shrinkage as a result of water saturation were explained by Collins (1939). Although that important study examined only the behavior of cotton, Harwood (1936) noted that linen fabrics could be expected to behave similarly. It was found that as water was absorbed into the fabric the transverse swelling of the fibers and yarns induced shrinkage in three ways: longitudinal fiber shrinkage, yarn shrinkage, and crimp accentuation. It is the third mechanism, however, that accounts for most of the canvas shrinkage.

The uptake of water by canvas fibers and yarns results in relatively large increases in their diameters (in typical cotton yarns, increases of 10% can be expected). Nevertheless, transverse swelling of fibers results in longitudinal shrinkages of only 1%. Yarn shrinkage, which is related to the degree of twist imparted on the yarn during spinning, can give rise to more shrinkage but accounts for shrinkages of only 2% in typical fabrics (Collins 1939). Hence, the shrinkage in the Sawyer portrait can be explained only by the crimp accentuation phenomenon.

The mechanism of crimp accentuation is illustrated in figure 2. Figure 2A represents the position of warp and weft yarns in an unrestrained fabric before wetting. When the fabric is wetted, swelling of both the yarns results. For the fabric to maintain the same external dimensions it had before wetting—that is, not shrink at all—the warp yarns would have to extend a given length (fig. 2B). The extension that would be necessary for the warp yarns to travel around the swollen weft yarns is represented by the shaded areas. There is an energetically simpler mechanism that accommodates the increased path of the warp yarns (fig. 2C). In this mechanism, the weft yarns move closer together and the warp path length remains the same. Likewise, an increase in the diameter of the weft yarns results in movement of the warp yarns closer together. For this reason, shrinkage of the fabric in both directions is observed.

From this description it is clear that construction has a significant bearing on a fabric's response to wetting. The degree of yarn twist, yarn diameter, and sizing have some influence, but the spacing of yarns (degree of crimp) is the most critical factor. Thus, the closer the yarn spacing and the more compacted the yarns, the greater the shrinkage effects (Gray 1971). The mechanization of the textile industry in the 19th-century gave rise to an abundance of tightly woven fabrics produced with power spinning and power weaving processes. This type of fabric shrinks more than a handmade fabric at high moisture levels.

Fig. 2. Fabric shrinkage mechanism due to wetting. Modified diagrams based on models presented by Collins (1939) and Gray (1971)

This mechanism of shrinkage in unrestrained fabrics also occurs in partially restrained fabrics such as the canvas support of a painting. There, movement is inhibited at the tack points but the rest of the fabric is free to respond to the internal forces generated.