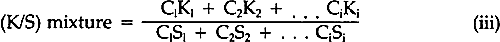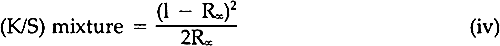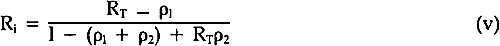2 BACKGROUND

THESE INVESTIGATIONS were first undertaken in 1962, and we have been further convinced, since that time, that many organic colorants in paint systems tend to fade according to first-order kinetics. In 1976, with the availability of modern computational techniques for colorant formulation, we designed a fifth series of experiments to study the kinetics of the fading of the widely used artists' pigment, alizarin lake, incorporating in this study many of the variables in the formulation of paint films. A few of the principal experimental results will be reported here for the case of opaque paint films made with a mixture of alizarin lake and titanium dioxide white pigment. Principally, we shall demonstrate that the process of fading of these opaque films can be described on the basis of first-order kinetics for the loss of alizarin lake as a function of exposure time.

The statement that the fading of a colorant system takes place according to “first-order kinetic behavior” means that the rate at which pigment is lost at any given moment is a constant fraction of the quantity of pigment present at that point in time. In other words, the rate of disappearance of the colored compound is proportional to its concentration. This is expressed mathematically as1:

Fig. .

Equation i may be expressed in the integrated form:

Fig. .

Fig. .

A review of the literature revealed only a few articles describing studies of the fading of pigmented or dyed materials in terms of chemical kinetics. In 1954, Haug suggested that paints often faded according to the first-order kinetic law, but his experimental data were not convincing and his work has rarely been cited.2 Baxter, Giles, and coworkers in the late 1950's, investigating films of molecularly-dispersed dyes in gelatin, methyl ethyl cellulose, and collodion, and measuring the changes in the concentration in terms of the logarithm of the absorbance of the dyes in the transparent films, showed that the rate of fading frequently followed first-order behavior.3,4 Several years later, Kortum used the Kubelka-Munk K/S function (Equation iv) to follow the thermally-induced fading of photo-darkened dyes absorbed on various substrates.5 Subsequently, the Kubelka-Munk function (Equation iv) was used to demonstrate that light-induced fading of dyes in pharmaceutical tablets followed the first-order law.6

In the results to be described, the relative amount of alizarin lake remaining in the light-exposed paint panels was computed by means of the Kubelka-Munk equations for opaque pigment mixtures7:

Fig. .

Fig. .

In order to solve Equations iii and iv, it is necessary to use the internal reflectance as R∞; this refers to the reflectance that would occur if there were no surface reflectance as a result of the refractive index differences between the paint medium and air. This is computed from the following equation8:

Fig. .

The K's and S's in Equation iii are the original absorption (K) and scattering (S) constants determined on the unexposed samples.7 From these characterized values, the concentrations (the C's) of the coloring matter in any mixture can be computed, using Equation iii and the measured reflectances of the exposed samples converted to K/S by Equation iv. The equation applies to a single wavelength of light only; hence, the reflectances at many wavelengths across the spectrum are necessary for the evaluation of the C's, solved simultaneously to fit the measured spectral data.

In a previous paper dealing with alizarin glazes (transparent or translucent films containing only alizarin-lake pigment), it was shown that use of the Kubelka-Munk equations appropriate to the case of films at incomplete hiding would permit prediction of the color changes occurring during the fading of glazes.10 The results to be reported here are those obtained, with alizarin lake mixed with a scattering white pigment, rutile titanium dioxide (TiO2), for the case of films made at complete hiding, that is, at a thickness so great that no light penetrates through the paint film to the substrate. The effect of a number of characteristic variables in paint formulation were investigated for both glazes and opaque films, but details of our findings with other variables must await subsequent publication.

It was our belief at the inception of this research that if the spectrophotometric curves of the original and of the faded states of a paint could be analyzed by colormatching computational techniques, it would then be possible to determine, for each faded state, the concentration of the original colored material that remained in a faded zone near the surface of the paints. In addition, if a new colorant of different hue were generated, the relative amount of the new colored substance could also be calculated. Thus, in order to obtain the concentrations of the colored components present at any given time during the course of the exposure of an alizarin lake-titanium white paint, we simply used a color-matching program to determine the percentage composition of pigments needed to “match” the color of the paint at each stage in the course of fading.