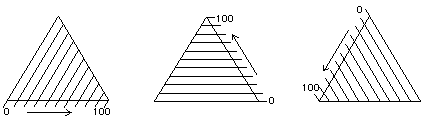Solubility Parameters: Theory and Application
by John BurkeSolvents are ubiquitous: we depend on them when we apply pastes and coatings, remove stains or old adhesives, and consolidate flaking media. The solubility behavior of an unknown substance often gives us a clue to its identification, and the change in solubility of a known material can provide essential information about its ageing characteristics.
Our choice of solvent in a particular situation involves many factors, including evaporation rate, solution viscosity, or environmental and health concerns, and often the effectiveness of a solvent depends on its ability to adequately dissolve one material while leaving other materials unaffected. The selection of solvents or solvent blends to satisfy such criterion is a fine art, based on experience, trial and error, and intuition guided by such rules of thumb as "like dissolves like" and various definitions of solvent "strength". While seat-of-the-pants methods are suitable in many situations, any dependence on experiential reasoning at the expense of scientific method has practical limitations. Although it may not be necessary to understand quantum mechanics to remove masking tape, an organized system is often needed that can facilitate the accurate prediction of complex solubility behavior.
Solubility Scales
Product literature and technical reports present a bewildering assortment of such systems: Kaouri-Butanol number, solubility grade, aromatic character, analine cloud point, wax number, heptane number, and Hildebrand solubility parameter, among others. In addition, the Hildebrand solubility parameter, perhaps the most widely applicable of all the systems, includes such variations as the Hildebrand number, hydrogen bonding value, Hansen parameter, and fractional parameter, to name a few. Sometimes only numerical values for these terms are encountered, while at other times values are presented in the form of two or three dimensional graphs, and a triangular graph called a Teas graph has found increasing use because of its accuracy and clarity.
Understandably, all this can be slightly confusing to the uninitiated. Graphic plots of solvent-polymer interactions allow the fairly precise prediction of solubility behavior, enabling the control of numerous properties in practical applications that would be very difficult without such an organizing system. Yet the underlying theories are often extremely complex, and an understanding of the "why" of a particular system can be very difficult, enough to discourage the use of such systems. Many of the systems mentioned, however, are actually quite simple (this is especially true of the Teas graph) and can be used to advantage with little understanding of the chemical principles at work.
This paper will attempt to bridge these two realities by briefly introducing solubility theory as well as its application so that the conservator will be both better able to understand and profitably apply the concepts involved. The discussion will center on Hildebrand solubility parameters and, after laying a theoretical foundation, will concentrate on graphic plots of solubility behavior. It should be remembered that these systems relate to non-ionic liquid interactions that are extended to polymer interactions; water based systems and those systems involving acid-base reactions cannot be evaluated by simple solubility parameter systems alone.
Solutions and Molecules
A solvent, usually thought of as a liquid, is a substance that is capable of dissolving other substances and forming a uniform mixture called a solution. The substance dissolved is called the solute and is usually considered to be the component present in the smallest amount. According to this definition, an almost-dry or slightly swollen resin film comprises a solution of a liquid (the solute) in a resin (the solvent), even though conventionally the liquid is usually referred to as the solvent, and the resin as the solute.
Molecular Attractions
Liquids (and solids) differ from gases in that the molecules of the liquid (or solid) are held together by a certain amount of intermolecular stickiness. For a solution to occur, the solvent molecules must overcome this intermolecular stickiness in the solute and find their way between and around the solute molecules. At the same time, the solvent molecules themselves must be separated from each other by the molecules of the solute. This is accomplished best when the attractions between the molecules of both components are similar. If the attractions are sufficiently different, the strongly attracted molecules will cling together, excluding the weakly attracted molecules, and immiscibility (not able to be mixed) will result. Oil and water do not mix because the water molecules, strongly attracted to each other, will not allow the weakly, attracted oil molecules between them.
Van der Waals Forces
These sticky forces between molecules are called van der Waals forces (after Johannes van der Waals who first described them in 1873). Originally thought to be small gravitational attractions, Van der Waals forces are actually due to electromagnetic interactions between molecules.
The outer shell of a neutral atom or molecule is composed entirely of negatively charged electrons, completely enclosing the positively charged nucleus within. Deviations in the electron shell density, however, will result in a minute magnetic imbalance, so that the molecule as a whole becomes a small magnet, or dipole. These electron density deviations depend on the physical architecture of the molecule: certain molecular geometries will be strongly polar, while other configurations will result in only a weak polarity. These differences in polarity are directly responsible for the different degrees of intermolecular stickiness from one substance to another. Substances that have similar polarities will be soluble in each other but increasing deviations in polarity will make solubility increasingly difficult.
Van der Weals forces, then, are the result of intermolecular polarities. As we shall see, accurate predictions of solubility behavior will depend not only on determining the result of intermolecular attractions between molecules, but in discriminating between different types of polarities as well. A single molecule, because of its structure, may exhibit van der Waals forces that are the additive result of two or three different kinds of polar contributions. Substances will dissolve in each other not only if their intermolecular forces are similar, but particularly if their composite forces are made up in the same way. (Such types of component interactions include hydrogen bonds, induction and orientation effects, and dispersion forces, which will be discussed later.)
The Hildebrand Solubility Parameter
It is the total van der Waals force, however, which is reflected in the simplest solubility value: the Hildebrand solubility parameter. The solubility parameter is a numerical value that indicates the relative solvency behavior of a specific solvent. It is derived from the cohesive energy density of the solvent, which in turn is derived from the heat of vaporization. What this means will be clarified when we understand the relationship between vaporization, van der Waals forces, and solubility.
Vaporization
When a liquid is heated to its boiling point, energy (in the form of heat) is added to the liquid, resulting in an increase in the temperature of the liquid. Once the liquid reaches its boiling point, however, the further addition of heat does not cause a further increase in temperature. The energy that is added is entirely used to separate the molecules of the liquid and boil them away into a gas. Only when the liquid has been completely vaporized will the temperature of the system again begin to rise. If we measure the amount of energy (in calories) that was added from the onset of boiling to the point when all the liquid has boiled away, we will have a direct indication of the amount of energy required to separate the liquid into a gas, and thus the amount of van der Waals forces that held the molecules of the liquid together.
It is important to note that we are not interested here with the temperature at which the liquid begins to boil, but the amount of heat that has to be added to separate the molecules. A liquid with a low boiling point may require considerable energy to vaporize, while a liquid with a higher boiling point may vaporize quite readily, or vise versa. What is important is the energy required to vaporize the liquid, called the heat of vaporization. (Regardless of the temperature at which boiling begins, the liquid that vaporizes readily has less intermolecular stickiness than the liquid that requires considerable addition of heat to vaporize.)
Cohesive Energy Density
From the heat of vaporization, in calories per cubic centimeter of liquid, we can derive the cohesive energy density (c) by the following expression
where:
c=Cohesive energy density
Δh=Heat of vaporization
r=Gas constant
t=Temperature
Vm = Molar volume
In other words, the cohesive energy density of a liquid is a numerical value that indicates the energy of vaporization in calories per cubic centimeter, and is a direct reflection of the degree of van der Waals forces holding the molecules of the liquid together.
Interestingly, this correlation between vaporization and van der Waals forces also translates into a correlation between vaporization and solubility behavior. This is because the same intermolecular attractive forces have to be overcome to vaporize a liquid as to dissolve it. This can be understood by considering what happens when two liquids are mixed: the molecules of each liquid are physically separated by the molecules of the other liquid, similar to the separations that happen during vaporization. The same intermolecular van der Waals forces must be overcome in both cases.
Since the solubility of two materials is only possible when their intermolecular attractive forces are similar, one might also expect that materials with similar cohesive energy density values would be miscible. This is in fact what happens.
Solubility Parameter
In 1936 Joel H. Hildebrand (who laid the foundation for solubility theory in his classic work on the solubility of nonelectrolytes in 1916) proposed the square root of the cohesive energy density as a numerical value indicating the solvency behavior of a specific solvent.
It was not until the third edition of his book in 1950 that the term "solubility parameter" was proposed for this value and the quantity represented by the symbol ∂. Subsequent authors have proposed that the term hildebrands be adopted for solubility parameter units, in order to recognize the tremendous contribution that Dr. Hildebrand has made to solubility theory.
Units of Measurement
Table 1 lists several solvents in order of increasing Hildebrand parameter. Values are shown in both the common form which is derived from cohesive energy densities in calories/cc, and a newer form which, conforming to standard international units (SI units), is derived from cohesive pressures. The SI unit for expressing pressure is the pascal, and SI Hildebrand solubility parameters are expressed in mega-pascals (1 mega-pascal or mpa=I million pascals). Conveniently, SI parameters are about twice the value of standard parameters:
| ∂/cal½cm-3/2 = | 0.48888 x ∂ /MPa1/2 | (3) |
| ∂/MPa½ = | 2.0455 x ∂ /cal½cm-3/2 | (4) |
Literature published prior to 1984 should contain only the common form, designated ∂, and it is hoped that where the newer SI units are used, they are designated as such, namely ∂/MPa½ or ∂(SI). Obviously, one must be careful to determine which system of measurement is being used, since both forms are called Hildebrand parameters. This paper will primarily use the SI values, and the use of standard values will be noted.
Solvent Spectrum
In looking over Table 1, it is readily apparent that by ranking solvents according to solubility parameter a solvent "spectrum" is obtained, with solvents occupying positions in proximity to other solvents of comparable "strength". If, for example, acetone dissolves a particular material, then one might expect the material to be soluble in neighboring solvents, like diacetone alcohol or methyl ethyl ketone, since these solvents have similar internal energies. It may not be possible to achieve solutions in solvents further from acetone on the chart, such as ethyl alcohol or cyclohexane—liquids with internal energies very different from acetone. Theoretically, there will be a contiguous group of solvents that will dissolve a particular material, while the rest of the solvents in the spectrum will not. Some materials will dissolve in a large range of solvents, while other might be soluble in only a few. A material that cannot be dissolved at all, such as a crosslinked three-dimensional polymer, would exhibit swelling behavior in precisely the same way.
Solvent Mixtures
It is an interesting aspect of the Hildebrand solvent spectrum that the Hildebrand value of a solvent mixture can be determined by averaging the Hildebrand values of the individual solvents by volume. For example, a mixture of two parts toluene and one part acetone will have a Hildebrand value of 18.7 (18.3 x 2/3 + 19.7 x 1/3), about the same as chloroform. Theoretically, such a 2:1 toluene/acetone mixture should have solubility behavior similar to chloroform. If, for example, a resin was soluble in one, it would probably be soluble in the other. What is attractive about this system is that it attempts to predict the properties of a mixture a priori using only the properties of its components (given the solubility parameters of the polymer and the liquids); no information on the mixture is required.
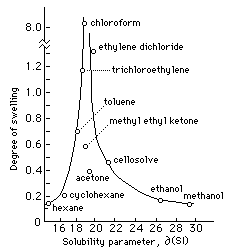
Fig. I Swelling of Linseed Oil Film in Solvents Arranged According to Solubility Parameter (adapted from Feller, Stolow, and Jones, On Picture Varnishes and Their Solvents)
Polymer Cohesion Parameters
Figure 1 plots the swelling behavior of a dried linseed oil film in various solvents arranged according to Hildebrand number. Of the solvents listed, chloroform swells the film to the greatest degree, about six times as much as ethylene dichloride, and over ten times as much as toluene. Solvents with greater differences in Hildebrand value have less swelling effect, and the range of peak swelling occupies less than two hildebrand units. By extension, we would expect any solvent or solvent mixture with a Hildebrand value between 19 and 20 to severely swell a linseed oil film. (The careful observer will notice certain inconsistencies in Fig. 1 which will be discussed later.)
Since a polymer would. decompose before its heat of vaporization could be measured, swelling behavior is one of the ways that Hildebrand values are assigned to polymers (the general term cohesion parameter is often preferred to the term solubility parameter when referring to non-liquid materials). Another method involves cloud-point determinations in which a resin is dissolved in a true solvent and titrated with another solvent until the mixture becomes cloudy, thus identifying the range of solubility. Testing cloud-points with a variety of solvents and diluents enable a precise determination of cohesion parameter values for polymers. Other methods include a combination of empirical tests, such as cloud-point and solubility/swelling tests, with the addition of theoretical calculations based on comparing chemical structure to other materials of known Hildebrand value.
Other Practical Solubility Scales
Similar empirical methods have been used to develop other solubility scales, unrelated to the Hildebrand parameter, that quantify solvent behavior. Many of these other systems have been developed for particular applications and are appropriate for use in those applications but, although agreement between unrelated systems is somewhat loose, it is possible to correlate most of these other systems to the Hildebrand parameter. While such correlations are not always practicable, it does support the Hildebrand theory as a unifying approach, and allows the translation of solubility information into whatever system is best for the application at hand.
Kauri-Butanol Value
A particularly common cloud-point test for ranking hydrocarbon solvent strength is the Kauri-Butanol test. The kauri-butanol value (KB) of a solvent represents the maximum amount of that solvent that can be added to a stock solution of kauri resin (a fossil copal) in butyl alcohol without causing cloudiness. Since kauri resin is readily soluble in butyl alcohol but not in hydrocarbon solvents, the resin solution will tolerate only a certain amount of dilution. "Stronger" solvents such as toluene can be added in a greater amount (and thus have a higher KB value) than "weaker" solvents like hexane.
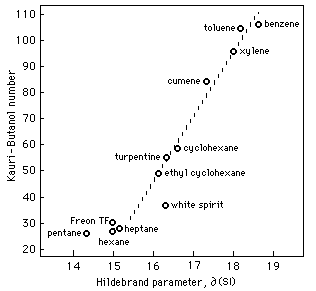
Fig. 2 Relationship Between Kauri-Butanol Number and Hildebrand Parameter
Figure 2 illustrates an almost direct relationship between KB values and Hildebrand values. This relationship is linear for solvents with KB values greater than 35 and can be expressed:
∂/MPa½= 0.04 KB + 14.2 (5)
For aliphatic hydrocarbons with KB values less than 35, the relationship, while also linear, involves calculations that include corrections for molecular size.
Solubility Grade
While the Kauri-Butanol test measures the relative strength of a solvent, another cloud-point test, developed by the National Gallery of Art Research Project, is used to determine the Solubility Grade of a polymer. In this test, 10% mixtures of the polymer in n-dodecane ( an aliphatic hydrocarbon, boiling point 213°C) are diluted with varying percentages of toluene. The Solubility Grade of the polymer is the minimum percent of toluene needed to give a clear solution, thus indicating the strength of the solvent needed to dissolve the polymer. The higher the percentage of toluene in the blend, the "stronger" is the solvent strength of the blend; the Solubility Grade is therefore the mildest blend that can be used to dissolve the polymer. Table 2 gives the Solubility Grades of several polymers, along with the corresponding Hildebrand number (SI) of the toluene-dodecane solution.
Although the Solubility Grade gives us a conveniently broad scale for judging the solubility of polymers in mild solvents, the Hildebrand value provides a slight additional advantage: the ability to assess the solubility of the polymer in solvent blends other than toluene-dodecane. To do this, the ratio is calculated of the relative contributions of the two new solvents in terms of their distance (in Hildebrand units) from the Hildebrand value of the polymer Solubility Grade. In this way we might determine that poly isobutyl methacrylate should form clear solutions above I0% solids in a solvent of heptane containing at least 42% xylene ( 16.53 -15.3)+(18.2 - 15.3). While the principle here is sound, it should be noted that the fine divisions between Hildebrand values in this instance can only give approximate results.
Other Solubility Scales
Other empirical solubility scales include the aniline cloud-point (aniline is very soluble in aromatic hydrocarbons, but only slightly soluble in aliphatics), the heptane number (how much heptane can be added to a solvent/resin solution), the wax number (how much of a solvent can be added to a benzene/beeswax solution), and many others. The aromatic character of a solvent is the percent of the molecule, determined by adding up the atomic weights, that is benzene-structured (benzene is the simplest hexagonal aromatic hydrocarbon). Benzene therefore has 100% aromatic character, toluene 85%, and diethyl benzene 56% aromatic character. By loose extension, the aromatic character of a mixed solvent, such as V.M. and P. naphtha or mineral spirits, is the percent of aromatic solvent in the otherwise aliphatic mixture.
These diverse solubility scales are useful because they give concise information about the relative strengths of solvents and allow us to more easily determine what solvents or solvent blends can be used to dissolve a particular material. Because most of these other systems can be more or less directly related to the Hildebrand solubility parameter, and because the Hildebrand solvent spectrum encompasses the complete range of solvents, it is the Hildebrand solubility parameter that is most frequently encountered in contemporary technical literature.
Component Polarities
As was mentioned above, there are inconsistencies in Fig. 1 that are difficult to explain in terms of single component Hildebrand parameters. The graph shows chloroform and ethylene dichloride (with Hildebrand values of 18.7 and 20.2 respectively) swelling a linseed oil film considerably more than methyl ethyl ketone (MEK) and acetone. And yet the Hildebrand values for MEK and acetone are 19.3 and 19.7, both between the values for the two high swelling solvents. Theoretically, liquids with similar cohesive energy densities should have similar solubility characteristics, and yet the observed behavior in this instance does not bear this out. The reason for this is the differences in kinds of polar contributions that give rise to the total cohesive energy densities in each case.
It was mentioned that van der Waals forces result from the additive effects of several different types of component polarities. The inconsistencies in Fig. 1 are due to the fact that, while the sum total cohesive energy densities are similar in the four solvents in question, the addends that make up those individual totals are different. These slight disparities in polar contributions result in considerable differences in solubility behavior. If these component differences are taken into account, quantified, and included in solubility theory, the prediction of solubility behavior can become more accurate. To do this, different types of polar contributions must be examined, and differentiated.
The following section is an introduction to the three types of polar interactions that are most commonly used in solubility theories: dispersion forces, polar forces, and hydrogen bonding forces. In some systems, the Hildebrand parameter is used in conjunction with only one or two of these forces (i.e. Hildebrand value and hydrogen bonding value), while more recent developments subdivide the Hildebrand parameter into all three forces, or derivatives of them. The concepts discussed provide an excellent foundation for understanding the inner workings of the practical systems introduced later. It should be stressed, however, that it is possible to use these practical systems without a thorough understanding of the molecular dynamics on which they are based.
Dipoles and Dipole Moments
Strong electromagnetic forces are present in every atom and molecule. At the center of a molecule is a positively charged atomic nucleus, while the outer surface is covered by a dispersed cloud of negatively charged electrons. These positive and negative charges balance out, and the molecule as a whole is neutral. If, for reasons we will investigate, the distribution of the electron cloud is uneven (maybe thicker in one place and thinner in another), small local charge imbalances are created: the parts of the molecule with a greater electron density will be negatively charged, and the electron deficient parts will be positively charged. The molecule as a whole, while still neutral, will have the properties of a small magnet, with equal but opposite poles, called dipoles.
A single molecule, because of its structure, can have several dipoles at once, some strong and some weak, some which cancel out, and some which reinforce each other. The resulting sum of all the dipoles is what is known as the dipole moment of the molecule. Molecules that have permanent dipole moments are said to be polar, while molecules in which all the dipoles cancel out (zero dipole moment) are said to be nonpolar.
This molecular polarity is at the heart of intermolecular attractions (imagine a pile of small magnets sticking together). The strength with which the molecules cling together, and therefore the cohesive energy density and the solubility parameter, is directly related to the strength of the molecular dipoles. But since the overall polarity of a molecule is often the combined result of several contributing polar structures, it is not enough to know the dipole moment of a molecule. The component polarities must be considered as well. Molecules like to be with other molecules of their own electromagnetic kind, both in terms of polar strength and in terms of polar composition.
Dispersion Forces
Nonpolar liquids, such as the aliphatic hydrocarbons, have weak intermolecular attractions but no dipole moment. Magnets without poles; how can this be? The source of their electromagnetic interactions can be described by quantum mechanics, and is a function of the random movement of the electron cloud surrounding every molecule. From instant to instant, random changes in electron cloud distribution cause polar fluctuations that shift about the molecular surface. Although no permanent polar configuration is formed, numerous temporary dipoles are created constantly, move about, and disappear.
When two molecules are in proximity, the random polarities in each molecule tend to induce corresponding polarities in one another, causing the molecules to fluctuate together. This allows the electrons of one molecule to be temporarily attracted to the nucleus of the other, and vise versa, resulting in a play of attractions between the molecules. These induced attractions are called London dispersion forces, or induced dipole-induced dipole forces.
The degree of "polarity" that these temporary dipoles confer on a molecule is related to surface area: the larger the molecule, the greater the number of temporary dipoles, and the greater the intermolecular attractions. Molecules with straight chains have more surface area, and thus greater dispersion forces, than branched-chain molecules of the same molecular weight. This dependence on surface area explains why conversions between Kauri-Butanol numbers and Hildebrand values for paraffin must include calculations for molecular size. The intermolecular forces between paraffin molecules are entirely due to dispersion forces, and are therefore size dependent.
Polar Forces
Dispersion forces are present to some degree in all molecules, but in polar molecules there are also stronger forces at work. Some atomic elements attract electrons more vigorously than others, and permanent dipoles are created when electrons are unequally shared between the individual atoms in a molecule. If the molecule is symmetrical, these dipoles may cancel out. If, on the other hand, the electron density is permanently imbalanced, with some atoms in the molecule harboring a greater share of the negative charge distribution, the molecule itself will be polar. The polarity of a molecule is related to its atomic composition, its geometry, and its size. Water and alcohol are strongly polar molecules, toluene is only slightly polar, and the paraffin hydrocarbons such as hexane and Stoddard solvent are considered to be nonpolar (again, the attractions between nonpolar molecules are due entirely to dispersion forces).
Polar molecules tend to arrange themselves head to tail, positive to negative, and these orientations lead to further increases in intermolecular attraction. These dipole-dipole forces, called Keesom interactions, are symmetrical attractions that depend on the same properties in each molecule. Because Keesom interactions are related to molecular arrangements, they are temperature dependent. Higher temperatures cause increased molecular motion and thus a decrease in Keesom interactions.
On the other hand, any molecule, even if nonpolar, will be temporarily polarized in the vicinity of a polar molecule, and the induced and permanent dipoles will be mutually attracted. These dipole-induced dipole forces, called Debye interactions, are not as temperature dependant as Keesom interactions because the induced dipole is free to shift and rotate around the nonpolar molecule as the molecules move. Both Debye induction effects and Keesom orientation effects are considered similar in terms of solubility behavior and are collectively referred to as polar interactions or simply polarities.
Hydrogen Bonding
A particularly strong type of polar interaction occurs in molecules where a hydrogen atom is attached to an extremely electron-hungry atom such as oxygen, nitrogen, or fluorine. In such cases, the hydrogen's sole electron is drawn toward the electronegative atom, leaving the strongly charged hydrogen nucleus exposed. In this state the exposed positive nucleus can exert a considerable attraction on electrons in other molecules, forming a protonic bridge that is substantially stronger than most other types of dipole interactions. This type of polarity is so strong compared to other van der Waals interactions, that it is given its own name: hydrogen bonding. Understandably, hydrogen bonding plays a significant role in solubility behavior.
The inconsistencies in Fig. 1 stem from a difference in hydrogen bonding between the chlorinated solvents and the ketones. The intermolecular forces in linseed oil are primarily due to dispersion forces, with practically no hydrogen bonding involved. These polar configurations are perfectly matched by the intermolecular forces between chloroform molecules, thus encouraging interpenetration and swelling of the linseed oil polymer. Acetone and methyl ethyl ketone, however, are more polar molecules, with moderate hydrogen bonding capabilities. Even though the total cohesive energy density is similar in all four solvents, the differences in component forces, primarily hydrogen bonding, lead to the observed differences. Acetone and MEK would much rather be attracted to each other than to linseed oil.
Two Component Parameters
A scheme to overcome the inconsistencies caused by hydrogen bonding was proposed by Harry Burrell in 1955. This simple solution divides the solvent spectrum into three separate lists: one for solvents with poor hydrogen bonding capability, one for solvents with moderate hydrogen bonding capability, and a third for solvents with strong hydrogen bonding capability, on the assumption that solubility is greatest between materials with similar polarities. This system of classification is quite successful in predicting solvent behavior, and is still widely used in practical applications. The classification according to Burrell may be briefly summarized as follows:
Weak hydrogen bonding liquids: hydrocarbons, chlorinated hydrocarbons, and nitrohydrocarbons.
Moderate hydrogen bonding liquids: ketones, esters, ethers, and glycol monoethers
Strong hydrogen bonding liquids: alcohols, amines, acids, amides, and aldehydes
Later systems assign specific values to hydrogen bonding capacity, and plot those values against Hildebrand values on a two dimensional graph. Although hydrogen bonding values are generally determined using IR spectroscopy (by measuring the frequency shift a particular solvent causes in deuterated methanol), another interesting method uses the speed of sound through paper that has been wet with the solvent being tested. Since paper fibers are held together largely by hydrogen bonds, the presence of a liquid capable of hydrogen bonding will disrupt the fiber-fiber bonds in preference to fiber-liquid bonds. This disruption of paper fiber bonding will decrease the velocity of sound travelling through the sheet. Water, capable of a high degree of hydrogen bonding, is used as a reference standard, and the hydrogen bonding value of a liquid is the ratio of its sonic disruption relative to water. In this test, alkanes have no effect on fiber hydrogen bonding, giving the same sonic velocities as air dried paper.
Hydrogen bonding is a type of electron donor-acceptor interaction and can be described in terms of Lewis acid-base reactions. For this reason other systems have attempted the classification of solvents according to their electron donating or accepting capability. Such extensions of the Hildebrand parameter to include acidity-basicity scales, and ultimately ionic systems, are relatively recent and outside the scope of this paper.
Three Component Parameters
Solubility behavior can be adequately described using Hildebrand values, although in some cases differences in polar composition give unexpected results (Fig. 1 , for example). Predictions become more consistent if the Hildebrand value is combined with a polar value (i.e. hydrogen bonding number), giving two parameters for each liquid. Even greater accuracy is possible if all three polar forces (hydrogen bonding, polar forces, and dispersion forces) are considered at the same time. This approach assigns three values to each liquid and predicts miscibility if all three values are similar.
As long as data is presented in the form of a single list, or even a two dimensional graph, it can be easily understood and applied. With the addition of a third term, however, problems arise in representing and using the information; the manipulation of three separate values presents certain inconveniences in practical application. It is for this reason that the development and the use of three component parameter systems has centered on solubility maps and models.
3-D Models
While polymer solubilities may be easily presented as a connected group of solvents on a list, or as a specific area on a graph, the description of solubilities in three dimensions is understandably more difficult. Most researchers have therefore relied on three-dimensional constructions within which all three component parameters could be represented at once.
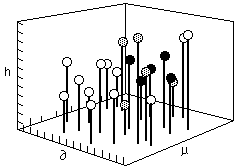
In 1966, Crowley, Teague, and Lowe of Eastman Chemical developed the first three component system using the Hildebrand parameter, a hydrogen bonding number, and the dipole moment as the three components. A scale representing each of these three values is assigned to a separate edge of a large empty cube. In this way, any point within the cube represents the intersection of three specific values. A small ball, supported on a rod, is placed at the intersection of values for each individual solvent ( Figure 3).
Fig. 3. A three dimensional box used to plot solubility information ( after Crowley, Teague and Lowe) a=Hildebrand value, p=dipole moment, h=hydrogen bonding value
Once all the solvent positions have been located within the cube in this way, solubility tests are performed on individual polymers. The position of solvents that dissolve a polymer are indicated by a black ball, nonsolvents by a white one, and partial solubilities are indicated by a grey ball. In this way a solid volume (or three dimensional area) of solubility is formed, with liquids within the volume being active solvents (black balls), and liquids outside the volume being non-solvents (white balls). Around the surface of the volume, at the interface between the area of solubility and the surrounding non-solvent area, the balls are grey.
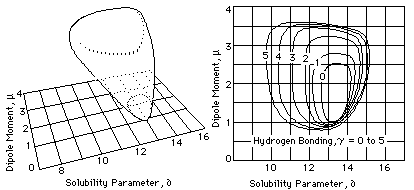
Once the volume of solubility for a polymer is established, it becomes necessary to translate that information into a form that is practical. This means transforming the 3-D model (difficult to carry around) into a 2-D graph (easier to publish). This is usually done in one of two similar ways. In both cases, the data is plotted on a rectangular graph that represents only two of the three component parameter scales (one side of the cube).
Fig. 4. Approximate Representations of Solid Model and Solubility Map for Cellulose Acetate (´from Crowley, at al, Journal of Paint Technology Vol 39, 504, Jan 1967) graph that represents either a single slice through the volume at a specified value on the third component parameter scale, or a topographic map that indicats several values of the third parameter at the same time (see Figure 4). Because the volume of solubility for a polymer usually has an unusual shape, several graphs are often needed for an individual polymer if its total solubility behavior is to be shown.
Maps such as these can' be used in conjunction with a table of three component parameters for individual solvents, and in this way provide useable information about solvent-polymer interactions and allow the formulation of polymer or solvent blends to suit specific applications. Data presented in this way is not only concise, but saves considerable time by allowing the prediction of solubility behavior without recourse to extensive empirical testing. !t is for these reasons that solubility maps are often included in technical reports and manufacturer's product data sheets. How graphs are actually used to accomplish these purposes will be described later in terms of the triangular Teas graph, in which these procedures are similar but greatly simplified.
Hansen Parameters
The most widely accepted three component system to date is the three parameter system developed by Charles M. Hansen in 1966. Hansen parameters divide the total Hildebrand value into three parts: a dispersion force component, a hydrogen bonding component, end a polar component. This approach differs from Crowley's in two major ways: first, by using a dispersion force component instead of the Hildebrand value as the third parameter, and second, by relating the values of all three components to the total Hildebrand value. This means that Hansen parameters are additive:
∂t2=∂d2 + ∂p2 + ∂h2 (6)
where
| ∂t2= | Total Hildebrand parameter |
| ∂d2= | dispersion component |
| ∂p2= | polar component |
| ∂h2 = | hydrogen bonding component |
The numerical values for the component parameters are determined in the following way: First, the dispersion force for a particular liquid is calculated using what is called the homomorph method. The homomorph of a polar molecule is the nonpolar molecule most closely resembling it in size and structure (n-butane is the homomorph of n-butyl alcohol). The Hildebrand value for the nonpolar homomorph (being due entirely to dispersion forces) is assigned to the polar molecule as its dispersion component value. This dispersion value (squared) is then subtracted from the Hildebrand value (squared) of the liquid, the remainder designated as a value representing the total polar interaction of the molecule ∂a (not to be confused with the polar component ∂p). Through trial and error experimentation on numerous solvents and polymers, Hansen separated the polar value into polar and hydrogen bonding component parameters best reflecting empirical evidence. Table 3 lists Hansen parameters for several solvents.
Hansen Model
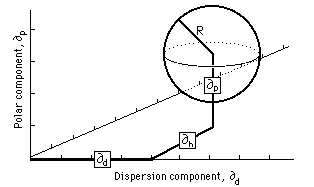
Charles Hansen also used a three-dimensional model (similar to that used by Crowley et al.) to plot polymer solubilities. He found that, by doubling the dispersion parameter axis, an approximately spherical volume of solubility would be formed for each. polymer. This volume, being spherical, can be described in a simple way (Figure 5): the coordinates at the center of the solubility sphere are located by means of three component parameters (∂d, ∂p, ∂h), and the radius of the sphere is indicated, called the interaction radius (R). Table 4 gives the Hansen parameters and interaction radius of several polymers.
Fig. 5, The Hansen volume of solubility for a polymer is located within a 3-D model by giving the coordinates of the center of a solubility sphere (∂d, ∂p, ∂h) and its radius of interaction (R). Liquids whose parameters lie within the volume are active solvents for that polymer.
A polymer is probably soluble in a solvent (or solvent blend) if the Hansen parameters for the solvent lie within the solubility sphere for the polymer. In order to determine this (without building a model) it must be calculated whether the distance of the solvent from the center of the polymer solubility sphere is less than the radius of interaction for the polymer:
D(S-P) = [4(∂ds - ∂dp)2 + (∂ps - ∂pp)2 + (∂hs - ∂hp)2]½ (7)
where
D(S-P) = Distance between solvent and center of polymer solubility sphere
∂xs=Hansen component parameter for solvent
∂xp=Hansen component parameter for polymer
(The figure "4" in the first term of equation (7), which doubles the dispersion component scale, is intended to create a spherical volume of solubility.) If the distance ( D(s-p) ) is less than the radius of interaction for the polymer, the-solvent would be expected to dissolve the polymer. This method avoids the reliance on graphic, plots of solubility behavior and can be used effectively in solely numerical form. The mathematics involved are inconvenient however (especially when solvent blends are concerned), and it is perhaps for this reason that the use of this excellent system is not more widespread.
Hansen Graph
Hansen parameters are both reasonably accurate in predicting solubility behavior and concise in their representation of that information.. Accurate because precise values for all three component parameters are utilized, and concise because the entire solubility volume for a polymer can be numerically indicated by four terms: one set of parameters and a radius.
On the other hand, a two-dimensional graph sacrifices some of that accuracy and conciseness in return for a system that clearly illustrates the relative positions of numerous materials, and can be easily used in practical applications. Predicting whether a polymer is soluble in a mixture of two solvents, for example, while possible mathematically, is accomplished on a graph by drawing a line between the two solvents and seeing whether that line passes through the area of solubility for the polymer.
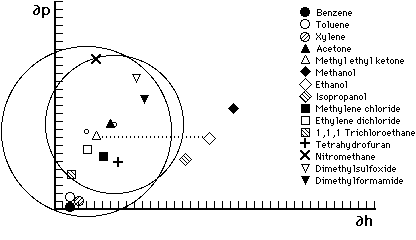
Figure 6. Hansen graph of solubility areas for poly(methyl methacrylate) (MMA) and poly(ethyl methacrylate) (EMA). Liquid parameters are indicated by symbols; small circles indicate center of solubility spheres. Liquids outside the solubility area of a polymer are non-solvents. The dotted line illustrates all the possible mixtures of MEK and ethanol—notice that MMA will tolerate a greater proportion of ethanol than will EMA Accordingly, MMA should be soluble in toluene/acetone 3:1, but not in 100% toluene.
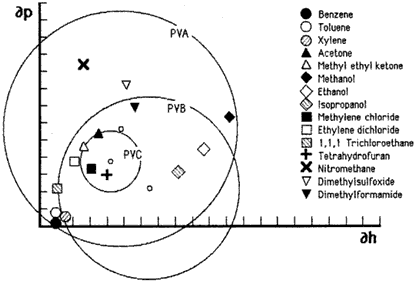
Figure 7. Hansen graph of solubility areas for polyvinyl acetate) (PVA), poly(vinyl butyral) (PVB), and poly(vinyl chloride). This type of graph uses only two of the three Hansen parameters.
As was the case with Crowley's solubility maps, Hansen's three dimensional volumes can be similarly illustrated in two dimensions by plotting a cross-section through the center of the solubility sphere on a graph that uses only two of the three parameters, most commonly ∂p and ∂h. Figures 6 and 7 illustrate this approach by plotting the volumes of solubility for five polymers: polyvinyl acetate, polyvinyl butyral, polyvinyl chloride, polymethyl methacrylate, and polyethyl methacrylate. The graphs use the hydrogen bonding component parameter and the polar component parameter as the X and Y axis, respectively, and plot the circle generated by the radius of interaction for each polymer; the symbols indicate the respective locations of solvents.
Hansen graphs are easy to use because solvent positions are constant and polymer solubility areas may be drawn with a compass; furthermore, solvent blending calculations can be done with a pencil and ruler. The accuracy of predicting solubility behavior is about 90%, with solvent locations nearest the edge of a solubility area being the least predictable. This is due to the three-dimensional nature of the actual solubility sphere. When reduced to two dimensions, solvents that appear near the edge inside the solubility area may in fact be outside it, in front or behind, in three dimensions.
Fractional Parameters
The division of the Hildebrand parameter into three component Hansen parameters (dispersion force, polar force, and hydrogen bonding force) considerably increases the accuracy with which non-ionic molecular interactions can be predicted and described. Hansen parameters can be used to interpret not only solubility behavior, but also the mechanical properties of polymers, pigment binder relationships, and the activity of surfactants and emulsifiers.
Being a three component system, however, places limitations on the ease with which this information can be practically applied. Translating this three component data onto a two-dimensional graph (by ignoring one of the components) solves this problem but sacrifices a certain amount of accuracy at the same time. What is n is a simple, planar graph on which polymer solubility areas can be drawn in their entirety in two dimensions. A triangular graph meeting these qualifications was introduced by Jean P. Teas in 1968, using a set of fractional parameters mathematically derived from the three Hansen parameters. Because of its clarity and ease of use, the Teas graph has found increasing application among conservators for problem solving, documentation, and analysis, and is an excellent vehicle for teaching practical solubility theory.
The Teas Graph
In order to plot all three parameters on a single planar graph, a certain departure must be made from established solubility theory. The construction of the Teas graph is based on the hypothetical assumption that all materials have the same Hildebrand value. According to this assumption, solubility behavior is determined, not by differences in total Hildebrand value, but by the relative amounts of the three component forces (dispersion force, polar force, and hydrogen bonding force)that contribute to the total Hildebrand value. This allows us to speak in terms of percentages rather than unrelated sums.
Hansen parameters are additive components of the total Hildebrand value (Equation 6). In other words, if all three Hansen values (squared) are added together, the sum will be equal to the Hild ebrand value for that liquid (squared). Teas parameters, called fractional parameters, are mathematically derived from Hansen values and indicate the percent contribution that each Hansen parameter contributes to the whole Hildebrand value:
In other words, if all three fractional parameters are added together, the sum will always be the same ( 100).
For example, the alkanes, with intermolecular attractions due entirely to dispersion forces, are represented by a dispersion parameter of 100, indicating totality, with both polar and hydrogen bonding parameters of zero. Molecules that are more polar have dispersion parameters of less than 100, the remainder proportionately divided between polar and hydrogen bonding contributions as the particular Hansen parameters dictate.
Because Hildebrand values are not the same for all liquids, it should be remembered that the Teas graph is an empirical system with little theoretical justification. Solvent positions were originally located on the graph according to Hansen values (using Equation 8), and subsequently adjusted to correspond to exhaustive empirical testing. This lack of theoretical foundation, however, does not prevent the Teas graph from being an accurate and useful tool, perhaps the most convenient method by which solubility information can be illustrated. Fractional parameters for solvents are listed in Table 6, at the end of this paper.
Figure 8. The Teas graph is an overlay of three solubility scales.
The Triangular Graph
The layout of a triangular graph is confusing at first to people who are accustomed to the common Cartesian rectangular coordinate graph. Instead of two axes perpendicular to each other, there are three axes oriented at 60º, and instead of these three axes requiring three dimensions in space, the triangular graph is flat. Furthermore, on a artesian graph all the scales graduate out from the same origin, but on a triangular graph the zero point of any one scale is the upper limit of another one.
This unusual construction derives from the overlay of three identical scales, each proceeding in a different direction (Figure 8). In this way, any point within the triangular graph uses three coordinates, the sum of which will always be the same: 100 (Figure 9).
Figure 9. At any point on a triangular graph, all three coordinates add up to 100.
Solvent Locations
By means of a triangular graph, solvents may be positioned relative to each other in three directions (Figure 10). Alkanes, whose only intermolecular bonding is due to dispersion forces, are located in the far lower right corner of the Teas graph, the corner that corresponds to 100% dispersion force contribution, and 0% contribution from polar or hydrogen bonding forces. Moving toward the lower left corner, corresponding to 100% hydrogen bonding contribution, the solvents exhibit increasing hydrogen bonding capability, culminating at the alcohols and water, molecules with relatively little dispersion force compared to their very great hydrogen bonding contribution. Moving from the bottom of the graph upwards we encounter solvents of increasing polarity, due less to hydrogen bonding functional groups than to an increasingly greater dipole moment of the molecule as a whole, such as the ketones and nitro compounds.
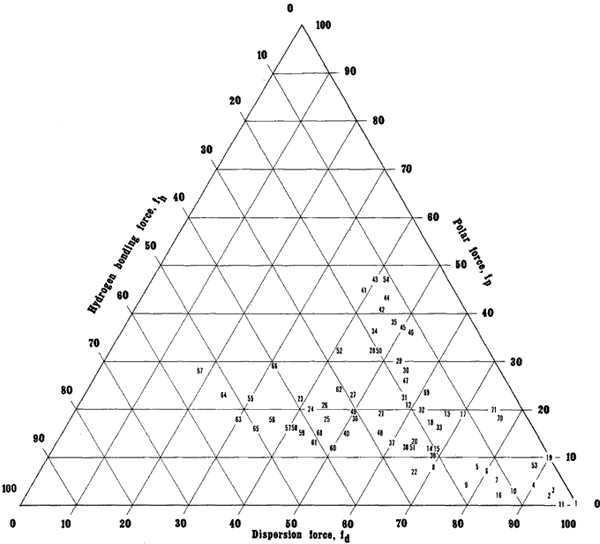
Figure 10. The Teas Graph
Numbers indicate solvent locations and refer to Table 5, pg. 43-45.
Overall, the solvents are grouped closer to the lower right apex than the others. This is because the dispersion force is present in all molecules, polar or not, and determining the dispersion component is the first calculation in assigning Hansen parameters, from which the Teas fractional parameters are derived. Unfortunately, this greatly overemphasizes the dispersion force relative to polar forces, especially hydrogen bonding interactions.
Solvent Classes
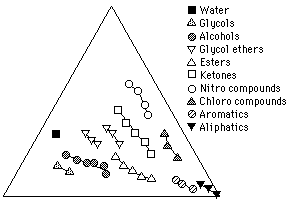
Figure 1 1 illustrates solvents on a Teas graph grouped according to classes. Increasing molecular weight within each class shifts the relative position of a solvent on the graph closer to the bottom right apex. This is because, as molecular weight increases, the polar part of the molecule that causes the specific character identifying it with its class, called the functional group, is increasingly "diluted" by progressively larger, nonpolar "aliphatic" molecular segments. This gives the molecule as a whole relatively more dispersion force and less of the polar character specific to its class.
Figure 11. Solvents grouped according to classes. Within each class, increasing molecular weight shifts the solvent position toward the right axis, corresponding to an increase in dispersion contribution relative to polar contributions.
This trend toward less polarity with increasing molecular weight within a class also accounts for the observation that lower molecular weight solvents are often "stronger" than higher molecular weight solvents of the same class, although determinations of solvent strength must really be made in terms of the solvents position relative to the solubility area of the solute. (Another reason for low molecular weight solvents seeming more active is that smaller molecules can disperse throughout solid materials more rapidly than their bulkier relatives.)
The only class in which increasing molecular weight places the solvent further away from the lower right corner is the alkanes. As previously stated, the intermolecular attractions between alkanes are due entirely to dispersion forces, and accordingly, Hansen parameter values for alkanes show zero polar contribution and zero hydrogen bonding contribution. Since fractional parameters are derived from Hansen parameters, one would expect all the alkanes to be placed together at the extreme right apex.
Observed behavior indicates, however, that different alkanes do have different solubility characteristics, perhaps because of the tendency of larger dispersion forces to mimic slightly polar interactions. For this reason, Teas adjusted the locations of the alkanes to correspond to empirical evidence, using Kauri-Butanol values to assign alkane locations on the graph. Several other solvent locations were also shifted slightly to properly reflect observed solubility characteristics.
The position of water on the chart is very uncertain, due to the ionic character of the water molecule, and the placement in this paper is according to recent published values (Teas, 1976). The presence of water in a solvent blend, however, can alter dramatically the accuracy of solubility predictions.
[It should be noted that the position of methylene chloride is also correct according to recent values. Many earlier publications have given methylene chloride incorrect parameters properly corresponding to Hansen's values for methyl chloride, a different chemical, possibly due to calculation error.]
Polymer Solubility Windows
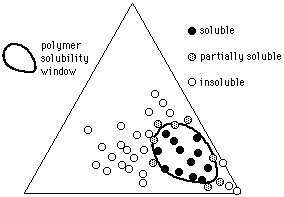
Given the solvent positions, it is possible to indicate polymer solubilities using methods similar to those used by Crowley and Hansen: a polymer is tested in various solvents, and the results indicated on the graph (a 3-D model is no longer necessary). At first, individual liquids from diverse locations on the graph are mixed with the polymer under investigation, and the degree of swelling or dissolution noted. Liquids that are active solvents, for example, might have their positions on the graph marked with a red dot. Marginal solvents might be marked with a yellow dot, and nonsolvents marked with black. Once this is done, a solid area on the Teas graph will contain all the red dots, surrounded with yellow dots (see Figure 12).
The edges of this area, or polymer solubility window, can be more closely determined in the following way. Two liquids near the edge of the solubility window are chosen, one within the window (red dot), and one outside the window (black dot). Dissolution (or swelling) of the polymer is then tested in various mixtures of these two liquids, using cloud-point determinations if accuracy is essential, and the mixture just producing solubility is noted on the graph, thus determining the edge of the solubility window. (The mixture would be located on a line between the two liquids, at a point corresponding in distance to the ratio of the liquids in the mixture.) If this procedure is repeated in several locations around the edge of the solubility window, the boundaries can be accurately determined. Interestingly, some composite materials (such as rubber/resin pressure sensitive adhesives, or wax resin mixtures) can exhibit two or more separate solubility windows, more or less overlapping, that reflect the degree of compatibility and the concentration of the original components.
Figure 12. The solubility window of a hypothetical polymer (circles indicate solvents).
This method of solubility window determination can be performed on samples under a microscope, and the results plotted on a Teas graph. In cases where the solubilities of artifactual materials are to be a prior to treatment, it is often unnecessary to delineate the entire solubility window of the materials in question. It can suffice to record the reaction of the materials to the progressive mixtures of a few selected solvents under working conditions in order to determine appropriate working solutions.
Temperature, concentration, viscosity
The solubility window of a polymer has a specific size, shape, and placement on the Teas graph depending on the polarity and molecular weight of the polymer, and the temperature and concentration at which the measurements are made. Most published solubility data are derived from 10% concentrations at room temperature.
Heat has the effect of increasing the size of the solubility window, due to an increase in the disorder (entropy) of the system. The more disordered a system is (increased entropy), the less it matters how dissimilar the solubility parameters of the components are. Since entropy also relates to the number of elements in a system (more elements=more disorder), polymer grades of lower molecular weight (many small molecules) will have larger solubility windows than polymer grades of higher molecular weight (fewer large molecules).
Concentration also has an effect on solubility. As stated, most polymer solubility windows are determined at 10% concentration of polymer in solvent. Because an increase in polymer concentration causes an increase in the entropy of the system (more elements=more disorder), solubility information can be considered accurate for solutions of higher concentration as well. Solvent evaporation as a polymer film dries serves to increase the polymer concentration in the solvent, thus insuring that the two materials stay mixed. It is possible, however, for polymer solutions of less than 10% to phase separate (become immiscible), due to a decrease in entropy. This is particularly susceptible to polymer-solvent combinations at the edge of the polymer solubility window. In other words, with lower polymer concentration there is an increase in the order of the system (less entropy); therefore, the size of the solubility window becomes smaller (there is less difference tolerated between solvent and polymer solubility values).
Solution viscosity also varies depending on where in the polymer solubility window the solvent is located. One might expect viscosity to be at a minimum when a solvent near the center of a polymer solubility window is used. However, this is not the case. Solvents at the center of a polymer solubility window dissolve the polymer so effectively that the individual polymer molecules are free to uncoil and stretch out. In this condition molecular surface area is increased, with a corresponding increase in intermolecular attractions. The molecules thus tend to attract and tangle on each other, resulting in solutions of slightly higher than normal viscosity.
When dissolved in solvents slightly off-center in the solubility window, polymer molecules stay coiled and grouped together into microscopic clumps which tend to slide over one another, resulting in solutions of lower viscosity. As solvents nearer and nearer the edge of the solubility window are used to dissolve the polymer, however, these clumps become progressively larger and more connected and viscosity again increases until ultimately polymer-liquid phase separation occurrs as the region of the solubility window boundary is crossed.
Dried film properties
The position of a solvent in the solubility window of a polymer has a marked effect on the properties of not only the polymer-solvent solution, but on the dried film characteristics of the polymer as well. Because of the uncoiling of the polymer molecule, films (whether adhesives or coatings) cast from solvent solutions near the center of the solubility window exhibit greater adhesion to compatible substrates. This is due to the increase in polymer surface area that comes in contact with the substrate. (Hildebrand parameters can be related to surface tension, and adhesion is greatest when the polarities of adhesive and adherend are similar.)
Many other properties of dried films, such as plastic crazing or gas permeability are related to the relative position that the original solvent occupied in the solubility window of the polymer. The degree of both crazing and permeability is predictably less when solvents more central to the solubility window have been used.
Evaporation rates and solubility
Solvent evaporation rates can also have a marked affect on dried film properties. The solubility parameters of solvent blends can change during film drying because of the difference in evaporation rates of the component liquids. If a volatile true solvent is mixed with a slow evaporating non-solvent, the compatibility between solvents and polymer can shift as the true solvent evaporates. The predominance of the non-solvent during the last stages of drying can result in a discontinuous, porous film with higher opacity and decreased resistance to water and oxygen deterioration. (There may be instances where these properties are desirable.)
This can be avoided, however, by either blending a small amount of a high boiling true solvent into the solvent mixture (this solvent remains to the last and insures miscibility), or by making sure that, if an azeotropic mixture is formed on evaporation, the parameters of the azeotrope lie within the polymer solubility window.
An azeotrope is a mixture of two or more liquids that has a constant boiling point at a specific concentration. When two liquids are mixed that are capable of forming an azeotrope, the more volatile liquid will evaporate more quickly until the concentration reaches azeotropic proportions. At that point, the concentration will remain constant as evaporation continues. If the position of the azeotropic mixture lies within the solubility window, compatibility with the polymer will continue throughout the drying process. This can be determined by consulting a table of azeotropes and checking the location of the mixture on the Teas graph in relation to the polymer solubility window. (Methods of plotting solvent mixtures are described in the next section.)
Blending solvents
Teas graph is particularly useful as an aid to creating solvent mixtures for specific applications. Solvents can easily be blended to exhibit selective solubility behavior (dissolving one material but not another), or to control such properties as evaporation rate, solution viscosity, degree of toxicity or environmental effects. The use of the Teas graph can reduce trial and error experimentation to a minimum, by allowing the solubility behavior of a solvent mixture to be predicted in advance.
Because solubility properties are the net result of intermolecular attractions, a mixture with the same solubility parameters as a single liquid will, in many cases, exhibit the same solubility behavior. Determining the solubility behavior of a solvent mixture, therefore, is simply a matter of locating the solubility parameters of the mixture on the Teas graph. There are two ways by which this may be accomplished: mathematically, by calculating the fractional parameters of the mixture from the fractional parameters of the individual solvents, and geometrically, by simply drawing a line between the solvents and measuring the ratio of the mixture on the graph. The mathematical method is the most accurate, and is appropriate for mixtures of three or more solvents. The geometrical method is the most convenient and is suitable for mixtures of two solvents, or for very rough guesses when three solvents are involved.
The mathematical method
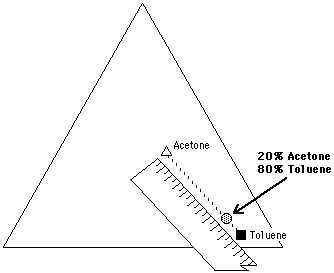
The solubility parameter of a mixture of liquids is determined by calculating the volume-wise contributions of the solubility parameters of the individual components of the mixture. In other words, the fractional parameters for each liquid are multiplied by the fraction that the liquid occupies in the blend, and the results for each parameter added together. For example, given a mixture of 20% acetone and 80% toluene:
In this way, the position of the solvent mixture can be located on the Teas graph according to its fractional parameters. Calculations for mixtures of three or more solvents are made in the same way.
The geometric method
The geometric method of locating a solvent mixture on the Teas graph involves simply drawing a line between the two solvents in the mix, and finding the point on the line that corresponds to the volume fractions of the mixture.
| fd | fd | fh | |
|---|---|---|---|
| Acetone: | 47 (x.20) = 9.4 | 32 (x.20) = 6.4 | 21 (x.20) = 4.2 |
| Toluene: | 80 (x.80) = 64.0 | 7 (x.80) = 5.6 | 13 (x.80) = 10.4 |
| 20/80 Mix: | fd =73.4 | fh =12.0 | fp = 14.6 |
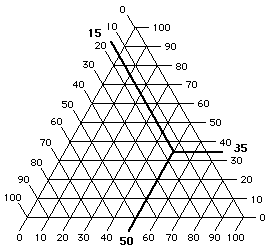
Figure 13. A mixture of 20% acetone and 80% toluene can be located on the Teas graph by using a pencil and ruler. The mixture lies on a line connecting the two liquids, at a distance equal to the ratio of the mixture, and closer to the liquid present in the greatest amount. This is illustrated in Figure 13 for the same 20% acetone, 80% toluene mixture. A line connecting acetone and toluene is drawn on the Teas graph. A point is then located on the line, 20% of the length of the line away from toluene. It is important to remember that the location of a mixture will be closer to the liquid present in the greatest amount.
Solvent blends and solubility windows
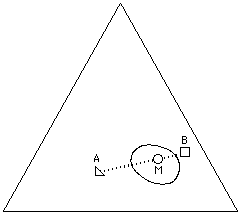
What is interesting about visualizing solvent blends on the Teas graph is the control with which effective solvent mixtures can be formulated. For example, two liquids that are non-solvents for a specific polymer can sometimes be blended in such a way that the mixture will act as a true solvent. This is possible if the graph position of the mixture lies inside the solubility window of the polymer, and is most effective if the distance of the non-solvents from the edge of the solubility window is not too great. This is illustrated in Figure 14.
Figure 14. A mixture (M) of non-solvents (A,B) may act as a true solvent for a polymer if the mixture is located inside the solubility window for the polymer on the Teas graph.
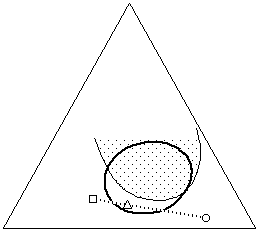
This phenomenon is particularly valuable when selective solvent action is required. Often it is necessary to selectively dissolve one material while leaving other materials unaltered, as in the case of removing the varnish from a painting, some adhesive tape from the image area of a print, or when a consolidant must not dissolve the material being consolidated. Sometimes the solubilities of all the materials involved are so similar that selecting an appropriate and safe solvent can be difficult. In such cases it is helpful to indicate the solubility windows of both the material that needs to be dissolved (varnish, adhesive, consolidant), and the materials that must be protected (media), on a Teas graph. This can be accomplished by simple solubility testing, noting the results of the tests on the graph.
Figure 15. In situations where one material must be dissolved (dark circle) while another must remain unaffected (shaded area), it is helpful to plot the solubility of both materials on the graph. A solvent blend can then be formulated (triangle) that selectively dissolves only the proper material (see text).
Once this has been done, it is easy to see the overlap of solubilities, and the areas where solubilities are mutually exclusive, if they exist. A solvent blend can then be formulated that actively dissolves the proper material, while positioned as far away from the solubility window of the other material as possible (Figure 15). It is important to remember that differences in evaporation rates can shift the solubility parameter of the blend as the solvents evaporate, and this must be taken into account. Additionally, while a material may not shown signs of solution in a solvent or solvent blend, the solvent may still adversely affect the material, for example by softening the material or leaching out low molecular weight components. Such changes can be irreversible and must be considered prior to embarking on a treatment.
Solvent mixture scales
Although the Teas graph is useful and informative when dealing with complex solubility questions, in most day to day situations choosing a solvent is a straightforward procedure that would be unnecessarily complicated by having to plot entire solubility windows. In most cases, the degree of solubility of a material is simply tested in various concentrations of two or three solvents, in order to determine the mildest solvent capable of forming a solution.
Perhaps the most often used solvent mixtures are blends of aliphatic and aromatic hydrocarbons, sometimes with the addition of acetone. This is because the search for the mildest solvent is often synonymous with the search for the least polar solvent (and the aliphatic hydrocarbons are the least polar possible).
Figure 16. Some common solvent blends (a=acetone, t=toluene, h=heptane, e=ethanol, m=methylene chloride, f=Freon TF). Inmost cases, dispersion force values give a relative indication of solvent strength (100=weakest, 30=strongest).
Testing whether a polymer is suitable for use in conservation, for example, usually involves determining the mildest solvent mixture that will dissolve both aged and un-aged samples. For this purpose, various concentrations of toluene in cyclohexane are used; should the polymer prove insoluble in straight toluene, however, increasing amounts of acetone are a until solubility is achieved. This type of solubility test anticipates the choices that will be made in working situations.
Looked at in terms of fractional parameters, what is being determined in such tests is essentially the location of the edge of the solubility window for the polymer in relation to, the lower right corner of the Teas graph. Figure 15 illustrates various mixtures of heptane, toluene, and acetone. It can been clearly seen that solvent strength increases with greater distance from the 100% dispersion axis. Blends of trichlorotrifluoroethane (Freon TF) and methylene chloride as well as blends of toluene ethanol are also illustrated. In all cases, increasing solvent strength follows decreasing dispersion force contribution.
For this reason, the use of fractional dispersion values (Table 5) is an excellent method for concisely designating relative solvent strength, in place of other more limited scales (Kauri-Butanol number, aromatic content, etc.). The benefits of this approach include the use of a standard designation that encompasses the entire range of solvent strengths, and the ability to easily enlarge the designation to include more precise solubility parameter data if necessary.
| % Heptane | % Toluene | % Acetone | Approx. fd |
|---|---|---|---|
| 100 | 0 | 0 | 100 |
| 75 | 25 | 0 | 95 |
| 50 | 50 | 0 | 90 |
| 25 | 75 | 0 | 85 |
| 0 | 100 | 0 | 80 |
| 0 | 85 | 15 | 75 |
| 0 | 70 | 30 | 70 |
| 0 | 55 | 45 | 65 |
| 0 | 40 | 60 | 60 |
| 0 | 26 | 76 | 55 |
| 0 | 10 | 90 | 50 |
| 0 | 0 | 100 | 47 |
Solvents and Health
As we have shown, the Teas graph can be a useful guide in tailoring solvent blends to suit specific applications. By adjusting the position of the blend relative to the solubility window of a polymer such properties as solution viscosity and adhesion can be optimized. Evaporation rates can be controlled independently of solvent strength, and the effects of temperature and concentration can be anticipated.
A further advantage that can be derived from this latitude in creating solvent mixtures is the possibility of choosing solutions based on degree of toxicity. A solvent mixture having a graph position close to another solvent will have such similar solubility characteristics to that solvent that it can be used interchangeably in many applications. For example, a petroleum solvent of 30% aromatic character is more or less the same whether the aromatic content is due to benzene (very toxic) or to toluene (moderately toxic). By extension, a mixture of ethanol/toluene 50:50 might be used in place of tetrahydrofuran in some applications, and toluene might be replaced with a 3:1 mixture of Stoddard solvent and acetone. In such cases, it should be pointed out that the similarity between solvents and blends having the same numerical parameters decreases as the distance between the components of the blend increases. Where alternate blends are effective, however, the use of a less toxic replacement can be a sensible choice, and the Teas graph a useful tool.
Conclusion
The theory of solubility parameters is a constantly developing body of scientific concepts that can be of immense practical assistance to the conservator. Through the media of solubility maps, complex molecular interactions can be visualized and understood, and in this way, solubility theory can simply function as a ladder to be left behind once the basic concepts are assimilated. On the other hand, the solution to an unusual problem can often be put within reach by graphically plotting solubility behavior on a Teas graph.
In the near future, the extension of solubility theory to encompass ionic and water based systems is conceivable, and the development of simple computer programs to manipulate multi-component solubility parameter data, along with accessible data bases of material solubilities, is probable. Until that time, both conservators and the objects in their charge can continue to profit by the use, either conceptual or real, of solubility parameter theory.
John BurkeThe Oakland Museum August 1984
References
Barton, Allan F. M., Handbook of Solubility Parameters end Other Cohesion Parameters Boca Raton, Florida: CRC Press, Inc., 1983.
Burrell, Harry, "The Challenge of the Solubility Parameter Concept," Journal of Paint Technology, Vol. 40, No. 520, 1968.
Crowley, James D., 0. S. Teague, Jr., and Jack W. Lowe, Jr., "A Three Dimensional Approach to Solubility," Journal of Paint Technology, Vol. 38, No. 496, 1966.
Durrans, Thomas H., Solvents. London: Chapman and Hall Ltd., 1971.
Feller, Robert L., Nathan Stolow, and Elizabeth H. Jones, On Picture Varnishes and Their Solvents. Cleveland: The Press of Case Western Reserve University, 1971.
Feller, Robert L., "The Relative Solvent Power Needed to Remove Various Aged Solvent-Type Coatings," in Conservation and Restoration of Pictorial Art, Bromelle and Smith, Eds., London: Butterworths 1976
Hildebrand, J. H., The Solubility of Non-Electrolytes New York: Reinhold, 1936
Hansen, Charles M., "The Three Dimensional Solubility Parameter Key to Paint Component Affinities: 1. Solvents Plasticizers, Polymers, and Resins," Journal of Paint Technology, Vol. 39, No. 505, 1967.
Hansen, Charles M., "The Three Dimensional Solubility Parameter - Key to Paint Component Affinities: 11. Dyes, Emulsifiers, Mutual Solubility and Compatibility, and Pigments," Journal of Paint Technology, Vol. 39, No. 51 1, 1967.
Hansen, Charles M., "The Three Dimensional Solubility Parameter - Key to Paint Component Affinities: 111. Independent Calculations of the Parameter Components," Journal of Paint Technology, Vol. 39, No. 511, 1967.
Hansen, Charles M., "The Universality of the Solubility Parameter Concept," I & E C Product Research and Development, Vol. 8, No. 1, 1969.
Hedley, terry, "Solubility Parameters and Varnish Removal: A Survey," The Conservator, No. 4, 1980.
Teas, Jean P., "Oraphic Analysis of Resin Solubilities," Journal of Paint Technology, Vol. 40, No. 516, 1968.
Teas, Jean P., Predicting Resin Solubilities. Columbus, Ohio: Ashland Chemical Technical Bulletin, Number 1206.
Torraca, Giorgio, Solubility and Solvents for Conservation
Problems Rome: ICCROM, 1978.
Publication History
Received: Fall 1984
This paper was submitted independently by the author, and was not delivered at the Book and Paper specialty group session of the AIC Annual Meeting. It has not received peer-review