Acidity: A Review of Fundamentals
by Harald BerndtIntroduction
Acidity is a topic of great concern to most conservators. Much research effort has been exerted on developing methods to deacidify paper and to evaluate the effects of these treatments. Many other areas of conservation are affected by the properties of acids and bases, since these influence the behavior of almost all chemical systems. This article reviews some fundamentals of the theory of acids and bases, and the measurement of acidity. It is intended as a basis for discussing specific applications of these concepts and, through the list of references, as a starting point for further research.
Acidity: Definition(s)
The term acid was probably derived from the Latin acidus, meaning sour to the taste, and referred specifically to vinegar (Jensen 1980). By the end of the 17th century, a number of physical and chemical properties was used to characterize acids, e.g. solubility in water and the ability to dissolve other substances. Robert Boyle added to that list the abilities to precipitate sulfur from sulfide solutions and to turn blue plant dyes red. In 1744, Rouelle introduced the term bases for a class of substances that reacts with acids to form salts (Finston and Rychtman 1982).
Acid-base reactions are of great importance in almost all areas of chemistry, and the historical development of acid-base theories is reviewed in most general chemistry textbooks. In chronological order, the theories of Arrhenius, Brønsted, and Lewis are probably the most influential. The theories have become more generalized, and the more recent ones can be thought of as including the older as special cases. The Lewis definition views acids as substances that can employ a lone electron pair of another molecule to complete their own electron structure and bases as being able to share an electron pair with another molecule. This may be written schematically as
| (Acid) + :(Base) | (1) |
The most important Lewis acid in the present context is the hydrogen ion, a single proton which has a radius smaller than that of any other ion by a factor of about 10,000. One consequence of the small size is a high charge density (i.e. electric charge per unit volume) which lets the proton exert greater polarizing power on its neighbors than any other similarly charged ion (e.g. sodium, Na+) (Bell 1973). The hydrogen ion provides the link to the Brønsted theory, which defines acids as substances with a tendency to donate protons and bases as substances with a tendency to accept protons. This definition can be schematically written as
| Acid1 | (2) |
After giving up a proton, the acid A can itself accept a proton and is by definition a base. The terminology is that an acid, after giving up a proton, turns into its conjugate base, B. Since the Brønsted (rather, Brønsted-Lowry) theory is more familiar to most than the Lewis theory, and since most practically important applications are based on it, all references to acid and/or base imply Brønsted acid and/or base.
Under practical conditions, the hydrogen ion cannot exist by itself and will always attach to a free electron pair of another atom. The molecule containing that atom then reacts by definition as a base. An exchange of a hydrogen ion is therefore synonymous with a reaction between an acid and a base. Any acid-base reaction has the form
| Acid1 + Base2 | (3) |
One says that acid1 is converted to its conjugate base1 and base2 is converted to its conjugate acid2.
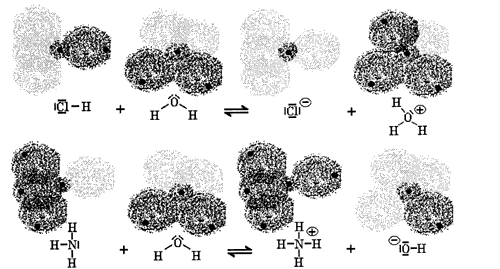
Many substances can react as acids or bases, depending on other substances present. The definition of acidity is therefore relative. An illustration of typical acid-base reactions, as well as of the ability of water to act as acid or base, is given in Figure 1.
Figure 1 Examples of acid-base reactions with water: towards hydrochloric acid (HCl), water reacts as a base, towards ammonia (NH3), it reacts as an acid.
Acidity and pH
With the use of thermodynamics and the Brønsted definition of acids and bases, the tendency to react as an acid can be quantified. According to the laws of thermodynamics, any chemical reaction establishes an equilibrium between the products and reactants, characterized by a number, K, called the chemical equilibrium constant. For the reaction given in Equ. 3, this number is given by
| K= | [Activity of Base1]
· [Activity of Acid2] | (4) |
| [Activity of Acid1] · [Activity of Base2] |
where activity is a measure of the availability of a substance for the reaction (see, e.g. Castellan 1971). The activity of a substance is related to its concentration by a factor, the activity coefficient which is a function of temperature and the activities of all other substances present.
Equ. 4 only measures the extent of acid-base reaction between one acid and one base. The majority of the important reactions occur in aqueous solution, and water can react readily either as acid or as base (see Figure 1). Therefore, one can use water as a common denominator and compare the strengths of other acids and bases by the extent of their reactions with water. For acids, the reaction used for comparisons is
| Acid1 +H2O | (5) |
The activities of reactants and products in this reaction can then be substituted in Equ. 4.
Equ. 4 can be simplified when one is interested in the behavior of substances in dilute aqueous solution, a very common condition. In dilute solutions, the activity coefficient of a substance approaches unity, and the concentration[1] of water can be considered constant. This results in a simpler expression for an equilibrium constant, given by
| Ka,w = | [Concentration of
H2OH+] ·[Concentration of
Base1] | (6) |
| [Concentration of Acid1] |
This is known as the acid dissociation constant in water whence the subscript a,w. Values of Ka,w or its negative decadic logarithm, pKa = -log10 K, can be found in the literature for many common substances (e.g. Weast 1978). Some examples are given in Table 1. Acids with K > 1 are considered strong, those with K < 10-4 are considered weak acids, and many substances are very weak acids.
Water can take the place of both acid1 and base2 in Equ. 3. It will react with itself to form its conjugate base (OH-) and its conjugate acid (H2OH+). The extent of this reaction is very small so that the water remains essentially pure, with a concentration of 55.55 mol/liter. A dissociation constant for water, Kw can then be defined as the product of the concentration of the conjugate acid ([H2OH+]) and the concentration of the conjugate base ([OH-]).
These concentrations must be the same and when they are measured conductimetrically one finds that
| [H+] = [OH] = vKw = 1.004 * 10-7 mol/l | (7) |
| Acidic molecule or ion | Ka,w | pKa |
|---|---|---|
| Bicarbonate anion (HOCO2-) | 3.98*10-7 | 10.40 |
| Carbon dioxide (CO2, in aq. sol'n) | 4.47*10-7 | 6.35 |
| Acetic acid (CH3COOH) | 1.76*10-5 | 4.75 |
| Formic acid (HCOOH) | 1.77*10-4 | 3.75 |
| Nitrous acid (HONO) | 5.89*10-4 | 3.23 |
| Sulphurous acid ((HO)2SO) | 1.54*10-2 | 1.81 |
| Nitric acid (HONO2) | 1.99*10+1 | - 1.30 |
| Hydrochloric acid (HCl) | 1.58*10+2 | - 2.20 |
More use can be made of the special properties of water if one recognizes that the strongest acid able to exist in appreciable concentration is the conjugate acid of water, H2OH+. If other acids, like those listed in Table I, are added to water and react to the extent indicated by their pKa, [H2OH+] increases and [OH-] then decreases so that their product remains constant. All this together then allows comparison of the acidities of all dilute aqueous solutions by measuring [H2OH+] only. As before with Ka,w, one uses the negative decadic logarithm because of the wide range of possible values and defines
| pH=-log10[H2OH+] | (8) |
Using this definition with the value of Kw, one finds that pure water has a pH of 7. The pH values of some common dilute aqueous solutions found in the literature (Weiss 1979, Streitwieser 1981) are shown in Table II. It can be seen that measuring the pH is a feasible way of comparing apples and oranges.
Though the concept of pH has meaning only for dilute aqueous solutions, Table II lists values for apparently solid materials like wood, paper or cheese. In all cases, however, only dilute aqueous solutions are measured. Food stuffs consist to a large extent of water, which may be extracted and used for pH determinations. Solids like paper and wood contain adsorbed water and, more importantly, water soluble substances, again allowing determination of a pH value by measurement of dilute aqueous solutions.
Measurement of [H2OH+]
After defining the concept of acidity and a quantitative expression for it, a method to evaluate the acidity of unknown solutions is the next concern. To this end, quantifiable properties of the concentration of hydrogen ions (rather: hydronium ions, H2OH+) must be found.
It is crucial to paper conservation that certain reactions, like the hydrolysis of cellulose, are catalyzed by the presence of H2OH+. Detailed discussions of this property can be found in Bell (1941). The speed of progress of an acid-catalyzed reaction is proportional to the concentration of H2OH+. This is used in very old but impractical methods of measuring acid strength.
The already mentioned property of acids to turn blue plant dyes red can be generalized and also be used to quantify [H2OH+]. This approach exploits the fact that some molecules, like blue plant dyes, change their color when they become protonated or deprotonated, i.e., change to their conjugate base or conjugate acid. Through relations like Equ. 6, the concentrations of acid and their conjugate bases are related to [H2OH+] or [OH-], which in turn are related through the same expression. Substances behaving in this manner, like the well-known litmus, are called indicators.
Through most of the range of possible pH values, an indicator will be present almost exclusively in either its acid or its base form. Only in a very narrow pH region will both forms be present at the same time. Any one indicator therefore is used only to determine whether a solution is below or above the pH value at which this particular indicator changes color. Indicator papers that allow determination of a range of pH values contain a mixture of several indicators, each of which changes color at a different pH.
Indicators can be put to use to determine acidities of systems other than dilute aqueous solutions by basing an acidity scale on the concentrations of the indicator's acid and base forms. An example is the Hammet acidity function (Rochester 1970), which defines a scale of actual acidity using the spectroscopically measured exact concentrations of indicator molecules in their protonated (HIn) and deprotonated (In) states. The value of the Hammet acidity function is then
given by
| H0 = pKa,w(HIn) - log10 | [HIn] | (9) |
| [In] |
Equ. 9 gives useful results only in a narrow range of actual acidity, where both forms of the indicator molecule are present in significant concentration. The useful range of this definition can be extended by using a sequence of chemically similar indicators with different pKa,w(HIn).
The method of [H2OH+] determination with the greatest practical significance makes use of another type of reaction in which H+ can partake. This involves the exchange of electrons (written usually as e-).The two so-called half-reactions
| A | (l0a) |
| B+ + e-
| (10b) |
are called oxidation (l0a) and reduction (10b). Their combination is known as an oxidation-reduction process or, more commonly, redox reaction. In Equ. (10), A is being oxidized while B is being reduced. As an example, in
| 2H2 | (11) |
| O2 + 4e-
| |
| 2H2 + O2
+ |
hydrogen is oxidized by oxygen, which in turn is reduced by the hydrogen, to form water.
If the two half-reactions of a redox reaction take place in spatially separated solutions, there will be a difference in the availability of electrons in the two solutions. If these two solutions are electrically connected, one can measure a voltage between them. This setup is the principle of galvanic cells (e.g., batteries). The voltage across a galvanic cell having:
| h+ + e-
| (12) |
as one half-reaction is proportional to the activity of protons in the solution being measured. The theory of such electrochemical pH determinations is discussed in detail by Bates (1973). An outline of the operational definitions of pH can be found in Weast (1978). Practical considerations like establishment of the required galvanic cell, and the equipment available are addressed by Westcott (1978).
Total Acid and Buffering
The three methods of measuring acidity discussed above, namely kinetic, colorimetric and electrochemical, compare the actual acidity of dilute aqueous solutions containing any number of components to that of pure water. An alternative approach of quantifying the acidity of a solution is to determine total acid or total alkali, respectively. To determine the total acid of a solution, small quantities of a strong base are added until the pH reaches a predetermined value, the so-called equivalence point where the amount of added base equals the amount of total acid in the solution. The base is added in the form of a dilute solution of known concentration. The process is known as acid-base titration. Sometimes the term neutralization is used but the equivalence point is not necessarily pH 7. The equivalence point is defined as the pH at which the amount of base added is equal to the amount of proton-donating molecules. For a particular acid, this point can be found by rearranging Equ. 6 and taking logarithms of both sides, which yields
| pH + pKa,w + log | [Base1] | (13) |
| [Acid1] |
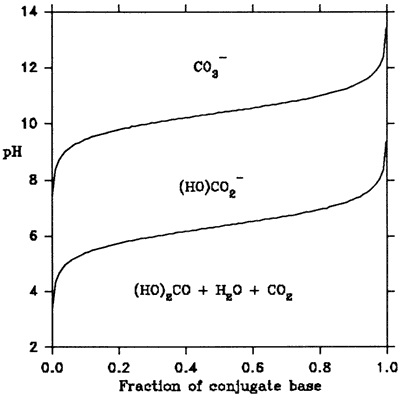
This is known as the Henderson equation (Mattock 1961). If one plots the resulting pH against the fraction of dissociated acid molecules, i.e., [Base1]/([Acid1]+[Base1), one gets the buffering curve for a particular acid. As an example, the buffering curves for the two conjugate bases of carbonic acid are shown in Figure 2. The figure shows that in order to deprotonate more than 95% of all carbonic acid molecules, titration should continue to above pH 12.
Acid-base titrations are very useful methods for quantifying acidity since they can be applied to systems other than dilute aqueous solutions, provided that a method for recognizing the equivalence point exists. Titrations may be used with suspensions of insoluble materials, allowing the determination of acidic groups in the molecules of the solids. The determination of the carboxyl content of pulp (TAPPI 1983) and of bound wood acid (Balaba and Subramanian 1984) use this technique. Other applications of acid-base titrations, as well as potential problems and errors, are discussed in detail by Kolthoff and Laitinen (1941) and by Mattock (1961).
Figure 2. Buffering curves of the dibasic acid (HO)2CO
The concept of buffering, mentioned above in the context of acid-base titrations, designates the property of a solution to show only negligible changes in pH on the addition of small quantities of strong acids or bases. Looking at Figure 2 again, one notices that over a sizeable range of values for the fraction of conjugate base, the pH changes very little. This shape is the reason for the name buffering curves.
The term buffered solution usually refers to a solution containing a weak acid and its salt, e.g., phosphate buffer containing (KO)(HO)2PO and (NaO)2(HO)PO. In such solutions, [Acid1] can be estimated as the total acid present and [Base1] as the amount of salt. The molarities of these can be substituted into Equ. 13 to calculate the resulting pH. Within limits, the pH can be varied by varying the relative concentrations. When a strong acid is added to a buffered solution, some of the Base1 ions accept the newly added protons, thereby increasing the concentration of Acid1. In this way, the chemical equilibria in the solution shift so as to maintain a stable pH.
Two quantities are frequently used to characterize buffering properties, the buffer capacity β and the dilution value ΔpHl/2. The buffer capacity is calculated as
| β = | Δ[H+] | (14) |
| ΔpH |
where Δ[H+] can be taken as equal to the amount of strong acid added to the solution. The dilution value,
| ΔpH1/2 = (pH)½ c - (pH)C | (15) |
is the difference between the pH of a solution diluted by an equal volume of water (pHl/2 c) and the pH of the original solution (pHc).
Actual Acidity of Insoluble Acids
Measurement of the total amount of insoluble acid has been discussed in the previous section. The actual acidity of these acids in pure water is not well defined and cannot easily be determined by the methods discussed so far. Since acid-base reactions in aqueous solutions are rapid, one can assume that the insoluble acids and the surrounding solution establish an equilibrium determined by the type of relations discussed previously. If the actual acidity of the insoluble acids and the surrounding solution are equal, no changes should occur. Hence, one can determine the actual acidity of insoluble acids, e.g. in wood or paper, by adding equal amounts of the material to be tested to a series of unbuffered solutions with varying pH. The solution whose pH remains unchanged has the same actual acidity as the material being tested. The basic procedure and some refinements have been described by Inguber (1958) and Stamm (1961).
Volatile Acids
Some acidic molecules like acetic acid and hydrochloric acid are volatile, i.e., they can exist in appreciable concentrations in an air space. Other molecules like CO2 or SO2 form acidic molecules upon absorption by water, in these cases (HO)2CO and (HO)2SO. The term vapor is generally used for substances present in solution and in the air. The concentrations of these substances in the solution and in the air are related by thermodynamic equilibria like those discussed above. Equilibrium is reached when the activities of the substance are the same in both phases. As long as the activity of a substance is higher in one phase than in the other, transport between the phases occurs, i.e., molecules are either absorbed into solution or desorbed into the gas phase. Adsorption-desorption equilibria are also established between surfaces and a liquid or gas phase.
Equilibria are of particular importance when substances of practically unlimited supply are involved. CO2 for example is present in all of the earth's atmosphere at a concentration of 0.033% by volume. It is therefore difficult to maintain CO2-free solutions. If (HO)2CO is neutralized by adding bases, some dissolved CO2 will be converted to (HO)2CO and new CO2 will be absorbed from the atmosphere. Over time, therefore, all alkaline solutions in equilibrium with the air space will eventually reach the pH of pure water in equilibrium with air, which is around pH 6 to 6.5. Similarly, in urban areas with consistently high concentrations of SO2 and NOX in the air, systems in equilibrium with that air will eventually reach the pH of pure water in equilibrium with the same air.
Summary
For most practical concerns, acids can be regarded as substances able to donate protons to other substances. Bases, then, are substances able to accept protons. Acids can accelerate chemical reactions, in particular, the hydrolysis of glycosidic bonds in cellulose. In dilute aqueous solutions, the actual acidity of the solution is the activity of the conjugate acid of water, H2OH+. The negative decadic logarithm of this activity is called pH and can be measured in several ways. The total acidity of a system can be determined by acid-base titration, provided the equivalence point can be determined. The actual acidity of systems that are not dilute aqueous solutions can be determined by the effect these systems have on unbuffered dilute aqueous solutions of given pH, brought into equilibrium with the system of interest.
Notes
1. Chemists use the shorthand "[A]" to denote the number of moles of A per liter of solution, which gives the molar concentration or molarity of the solution.
References
Balaba, W. M. and R. V. Subramanian. 1984. The acidity of bound wood acid: a new method for determining the acidity of insoluble acids. Holzforschung 38(6): 309-312.
Bates, R. G. 1973. Determination of pH, theory and practice. Second edition. New York, NY: Wiley-Interscience.
Bell, R. P. 1973. The proton in chemistry, 2nd edition. Ithaca, NY: Cornell University Press.
Bell, R. P. 1941. Acid-base catalysis. Oxford: The Clarendon Press.
Castellan. G. W. 1971. Physical chemistry, second edition. Reading, MA: Addison-Wesley Publishing Company.
Finston, H. L. and A. C. Rychtman. 1982. A new view of current acid-base concepts. New York, NY: Wiley-Interscience.
Ingruber, O. V. 1958. The behavior of wood and wood constituents as acid-buffering systems. Pulp and Paper Magazine of Canada 59(11): 135-141.
Jensen, W. B. 1980. The Lewis acid-base concepts. New York, NY: Wiley-Interscience.
Kolthoff, I. M. and H. A. Laitinen. 1941. pH and electro titrations, second edition. New York, NY: Academic Press.
Mattock, G. 1961. pH measurement and titration, London: Heywood and Company, Ltd.
Rochester, C. H. 1970. Acidity functions. In Organic chemistry, a series of monographs, vol. 17. New York, NY: Academic Press
Stamm. A. J. 1961. A comparison of: Three methods for determining the pH of wood and paper. Forest Products Journal 11(7): 310-312.
Streitwieser, A. and C. H. Heathcock. 1981. Introduction to organic chemistry. New York, NY: Macmillan Publishing Co., Inc.
TAPPI. 1983. Carboxyl content of pulp. TAPPI Standard T 237 om-83.
Weast, R. C. and M. J. Astle, eds. 1978. CRC handbook of chemistry and physics, 59th edition. Boca Raton, FL: CRC Press, Inc.
Westcott, C. C. 1978. pH measurements. New York, NY: Academic Press.
Harald BerndtAssistant Specialist
Timber Mechanics/Wood Artifacts Conservation Group
University of California Forest Products Laboratory
Publication History
Received: Fall 1991
This paper was submitted independently by the author, and was not delivered at the Book and Paper specialty group session of the AIC Annual Meeting. It has not received peer-review