Gesso's interparticle bond is modeled as a function of gesso recipe. Mechanical properties of gesso become predictable from that of glue alone. Cracking of gesso perpendicular to the grain on wood results from drying stresses plus wood shrinkage across the grain plus insufficient stress relaxation in the glue at low humidity.
Some gilding cracks, some does not, even after centuries. It is generally accepted that relative humidity fluctuations are somehow the cause for the cracking of gilding, but no clear explanation exists. This paper explores two levels of explanation--macroscopical and microscopical--with the ultimate intent of producing estimates of permissible humidity fluctuations for old gilding and guidelines for durable new gilding. It is part of a larger project on the mechanical properties of painting materials, currently under way at the Canadian Conservation Institute, in which gilding is considered as a particular use of gesso and gesso as a particularly important pigmented coating.
The simplest explanatory model, movement of wood under an inert gesso, leads to the prediction that cracking will occur parallel to the wood grain. Gilding does crack this way sometimes, but the commonest cracks run perpendicular to the grain.
Another hypothesis is that gesso shrinks in both directions as much as wood does across the grain (about 1%-2% for a 50% RH drop), so a differential arises only along the grain. Claudia Deschu disproved this by showing that shrinkage of a free-hanging gesso for a 40% RH drop was less than 0.05% (the approximate sensitivity of her apparatus).1
Deschu proposed an alternate mechanism, having noted that her loose strips of gesso shrank noticeably between the firm damp stage and t he fully dry stage. Since gesso sticks to the wood partway through drying, subsequent shrinkage results in what the paint industry calls internal stress.2 If internal stress is uniform in all directions, then narrow pieces of wood may simply develop cracks across the shortest route from edge to edge. Narrow bands of gesso or compo probably follow this model, but the model does not explain the crack pattern of Victorian oval inner frames: cracks lie across the grain despite the shortest route. The same is true of large pieces of gilded furniture: cracks carefully follow changes in wood grain.
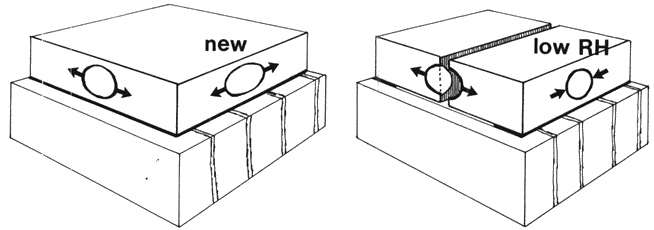
A plausible explanation of this phenomenon is the combination of residual stress and shrinkage of the wood. The hypothetical forces are illustrated in figure 1. The image on the left shows new gesso drying with internal stress. That on the right shows how with low RH the wood shrinks across the grain, thereby releasing stress in this direction, while the stress along the grain is not released--indeed, it increases because gesso stiffness increases. Cracks start at the edge and grow across the grain.
Fig. 1. The macroscopical model of gesso on wood: (left) as manufactured and (right) at low humidity. The two bubbles represent edge flaws where cracks can start.
For stress to grow a crack from some flaw, there must be movement. Although that sounds facile, it implies that either the gesso delaminates as proposed in figure 1, or it shears internally to produce a tapered crack, like a check in wood. Most cracks I have seen in thin gesso do not appear tapered, so delamination must have either preceded or coincided with cracking. Gesso may check on first drying when applied too thickly, as may compo after years because the oil component continues to shrink.
The Role of the Gold Leaf Gold leaf contributes no strength to the gilding, but it does form a perfect vapor barrier, except for holes. The holes, in turn, have a permanence dependent on the bole and gesso below. Since bole contains laminar particles in enough medium to make a paste, it will be much less permeable than gesso and will determine the permanence of each hole. The hygroscopic response of the entire object is then characterized by the hygrometric halftime (t1/2), which for a wood plank gilded all around becomes:
where  is
the slope of EMC/RH curve, ~0.1;
is
the slope of EMC/RH curve, ~0.1; 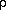 is the density of wood, ~500
kg/m3;1 is the thickness of wood; ps is the
saturation vapor pressure, 2337 Pa at 20°C; f is the fractional
area of holes in leaf; and M is the permanence of bole.
is the density of wood, ~500
kg/m3;1 is the thickness of wood; ps is the
saturation vapor pressure, 2337 Pa at 20°C; f is the fractional
area of holes in leaf; and M is the permanence of bole.
A conservative estimate of the permanence of bole will be that of ordinary latex paint--that is, 3 E-10 kg/m1 Pa s. I examined by microscope single-leaf gilding from a student's work and found pinholes with diameters about a tenth of their spacing apart, that is, 1% of the area. This would be a generous estimate for most gilding in good condition. Pieces gilded on one side, or with bare end grains, have a hygrometric halftime given by
where l is the dimension perpendicular to the bare face; n is 1 or 2 bare faces; D is diffusion coefficient of wood perpendicular to the bare face (4.6 E-11 m2/s across grain 2.7 E-9 m2/s along grain) at 50% RH.3
| Wood | Gilding | Halftime |
| 1 cm-thick plank | All but 1 side |
5 days with good air access; longer if air access is limited |
| 30 cm-long post | All but both ends, any diam. | 20 days with good air access; longer if air access is limited |
| 1 cm-thick plank or 3 cm-diam. post | All | 3,000 days if f=0.1% 300 days if f=1.0% 30 days if f=10.1% |
Table 1 shows response times for typical gilded geometries. Wood gilded all around (for example, furniture) could be immune to seasonal humidity fluctuations if the ends were sealed well, with, for example, leaf, other metal foil, wax, or Saran. Wood gilded on one side only (for example, picture frames, which normally have bare wood on the underside) will respond within a week. Since on picture frames these bare surfaces are hidden from view, the application of a vapor barrier to those bare surfaces would not be problematic and would be the simplest way to eliminate humidity effects.
Because gold leaf is such a good vapor barrier, the moisture content of the gesso stays in quasi equilibrium with the wood underneath. Accordingly, moisture gradient cannot be part of any explanation of cracking or cupping in gilding.
Pigment Volume Concentration
Gesso is a type of paint. Most paint properties depend ultimately on the microscopical geometry of particles and binder, and one parameter characterizes it best: ..pigment volume concentration (PVC). The term pigment here refers to all particles, regardless of whether they are good colorants.
where P is pigment volume, and B is binder volume.4 The space between particles and binder is termed the porosity φ
where C is the void volume.
The first set of experiments was carried out on small pieces of wood (8 cm x 8 cm x 6 mm) that were water gilded in a traditional fashion on the face, then oil gilded around the edges. The back were left bare. (Gilding was done under the supervision of Gordon Fairbairn at Canadian Conservation Institute.) The RH during fabrication was 50%. They were then exposed to 5% RH for one week. They curved, but no cracks appeared. One was exposed to 90% RH for a week then returned to 5% RH. There were no cracks. Notches were made with a scalpel; there were no cracks. One was exposed to -50°C for weeks, another to 100°C (both bagged). One was left at 5% RH for two years--nothing. Clearly, well--prepared new gilding does not necessarily crack with exposure to one humidity or temperature cycle.
At this point, I returned to the "beginning" experimentally to separate variables. Gesso was prepared from industrial whiting (precipitated calcium carbonate) and rabbit-skin glue. The ratio of total liquid to whiting was kept constant at 1:1 by weight, and the glue concentration varied. The slurries were prepared warm, and each was cooled until it began to thicken. Draw downs were made 8 cm wide on 40 cm glass plates. The draw blade was set 2 mm high on one side and 0 mm on the other, thus casting a tapered gesso. The glass plates had three different surfaces: 1/3 had been sprayed with a dry release agent (poor adhesion), 1/3 had been sprayed with the same agent through a coarse screen that was 30% open (moderate adhesion), and 1/3 was clean (good adhesion). Draw downs were made at PVCs of 90%, 92%, 94%, 96%, 98%, and 99%--that is, from a typical softwhite/intermediate recipe through to unusable soft recipes.
After drying for two days at 50% RH, the gesso films showed no delamination or noticeable cracks. The two softest gessoes, 98% and 99% PVC, showed tiny crowfoot checks around some bubbles. Samples were then exposed to 5% RH. The 92% and 90% PVC samples delaminated and cracked; the others were unaffected.
Fig. 2. Stages in delamination and cracking of gesso on glass plates.
Figure 2 shows the general stages. Delamination always ; occurs first from the thick edge and from several sites (1). Not until delamination was 1 cm to 4 cm long did cracks initiate (2). When areas of delamination merged, the apexes of the delaminating front moved to the crack tips (3). Stages 1, 2, and 3 took less than an hour. (Table 2 summarizes the results.) The samples were then exposed to 90% RH overnight, placed in 5% RH ( for a day, and finally returned to 50% RH. Some delamination proceeded slightly further, but the main effect was to shrink the already delaminated gesso, thus widening the old cracks and bifurcating their tips (4). The shrinkage of long fragments on each sample was then measured (by microscope) at points B, by comparison with traces of thin gesso left on the glass. Fragments were then broken along the edge of the delamination, thereby releasing any internal strain, and shrinkage was measured across points A the next day.
The gesso-on-glass experiment illustrated the following: Internal stress of gessoes in the softwhite range (99%-90% PVC) dried at 50% RH is insufficient to cause delamination even when poorly adhered to its substrate. Desiccation to 5% RH increases stress significantly: the harder gessoes in this range delaminated if adhesion was inadequate. With poor adhesion, the thinnest layers detached; with good adhesion, the thickest layers (0.7 mm) remained. Moderate adhesion gave partial delamination. Whenever the . gesso delaminated, it cracked, although nondelaminated gesso must have been under the same general stress. Apparently, flaws cannot stretch enough to start a crack while the gesso is still attached to the substrate. The experiment also showed that high humidity shrinkage dramatically widens cracks between loose gesso but changes the behavior of attached gesso only slightly.
Fig. 3. Stress in a gesso film, 90% PVC, during drying, and over time at 50°6 RH, 21°C.
Drying stress was measured directly as follows: Pieces of rough aluminum sheet (1.5 mm) were clamped in each jaw of a horizontal tensile tester, so that 3 cm stuck out. The jaws were set 34 cm apart, and a 3 cm x 30 cm strip of polyethylene film was adhered to the aluminum sheets. The slack was taken up by 140 g force (only about 101/6 of the force the gesso developed). 'The polyethylene was supported temporarily from below, and a 90% PVC gesso was drawn down (0.5 mm when dry). The gesso at each end was fanned to speed drying and maintain an adequate bond to the aluminum. After drying, the sample was exposed to 90% RH overnight, and tension was monitored over the long team. Unfortunately, the sample was not monitored frequently, and it broke during a lab shuffle a year later. Crack width was measured six months later.
| Sample | 99%, 98%, 96%, 94% PVC | 92% PVC | 90% PVC |
| Poor adhesion surface | No delamination | Total delamination | Total delamination |
| Moderate adhesion surface | No delamination | 2/3 delamination that stops at 0.4 mm thick | 2/3 delamination that stops at 0.4 mm thick |
| Good adhesion surface | No delamination | Very slight delamination that stops at 1.0 mm thick | 1/2 delamination that stops at 0.3 mm thick |
| Shrinkage at A in fig. 2 | Not applicable | 0.13% (±0.4) | 0.1796 (±0.6) |
| Shrinkage at B in fig. 2 | Not applicable | 0.78% (±0.5) | 0.9596 (±0.05) |
| Shrinkage of sample in stress tester | Not applicable | Not applicable | 0.16% (±0.01) |
| Recipe | Cg (%) | PVCgel(%) | Sgel/d | PVCdry (%) | Sdry/d |  RHx E + 3 RHx E + 3 |
 break (%) break (%) | |||
| 10% glue solution | Water | Whiting | ||||||||
| Clearcole | 2.0 | 1.0 | 0.63 | 6.7 | 7 | 1.20 | 58 | 0.200 | 6.64; 6.6* | 0.40; 0.3* |
| Hardwhite | 2.0 | 1.0 | 2.00 | 6.7 | 20 | 0.55 | 82 | 0.086 | 2.56; 2.6* | 0.15; 0.2* |
| Softwhite | 1.5 | 1.5 | 3.00 | 5.0 | 27 | 0.40 | 90 | 0.035 | 1.38 | 0.08 |
| Intermediate | 0.5 | 2.5 | 3.00 | 1.7 | 27 | 0.40 | 96 | 0.012 | 0.54 | 0.03 |
*Measured by Marion F Mecklenburg, "Some Mechanical and Physical Properties of Gilding Gesso," figs. 3, 4, 11, 12, elsewhere in this volume.
The drying stress test, plotted in figure 3, showed the following: About 25% of the stress develops slowly during the damp, gray phase, arid 75% develops quickly during the white phase. Exposure to high RH will increase stress by 50%.5 The year-long measurements are plotted logarithmically, the usual manner for stress relaxation. They show that stress relaxation near 50% RH does not reduce stresses from daily or weekly RH fluctuations by more than 25%, but after three months, stress relaxation increases dramatically. Although there is inadequate data here to support the curve as shown, the curve is based on the known visco-elastic behavior of gelatin that is discussed below.
Fig. 4. The microscopical model of gesso: whiting particles and glue binder (to scale for 80% PVC).
Applied gesso cools quickly to the object temperature, and it gels. Typical gessoes for gel binders are 20%-27% PVCwet (table 3). Interparticle separation in the gel becomes 0.4 diam. to 0.6
where Sgel is the particle separation and d is the particle diameter. Figure 4 shows the particle separation in the gel and the coalescence when dry. The particles are well separated at the start of drying. The binder dries as a semirigid gel rather than a viscous liquid, and the gel maintains the relative position of glue molecules as much as possible during drying. Since most of the gel can be assigned to separate shells around each particle, drying can be envisaged as the shrinkage of these shells. Thus interparticle separation in dry gesso (Sdry) can be calculated as:
Shrinkage with RH then depends on the disks of glue between
particles. Given the definition of shrinkage coefficient,  RH:
RH:
where RH0 is the RH at manufacture of the object, then by equation 6:
Marion Mecklenburg's experimental graph elsewhere in this volume
yields  RH,glue,=0.040 (a similar value is obtained
using 1/3 the EMC/RH slope of gelatin).6 I have calculated the coefficients of the
various gessoes for table 3 under the column
RH,glue,=0.040 (a similar value is obtained
using 1/3 the EMC/RH slope of gelatin).6 I have calculated the coefficients of the
various gessoes for table 3 under the column  RH,
gesso. Mecklenburg's experimental values shove excellent agreement.
The predicted values for the softwhite gesso explain Deschu's
negative results: such recipes would move less than the sensitivity
of her apparatus. Similarly, elongation at break (%
RH,
gesso. Mecklenburg's experimental values shove excellent agreement.
The predicted values for the softwhite gesso explain Deschu's
negative results: such recipes would move less than the sensitivity
of her apparatus. Similarly, elongation at break (% break) for the gessoes can be predicted based
on that of glue itself under similar test conditions (2.4%) and
equation 8. These are also given with Mecklenburg's data in table
3,, and agreement is good.
break) for the gessoes can be predicted based
on that of glue itself under similar test conditions (2.4%) and
equation 8. These are also given with Mecklenburg's data in table
3,, and agreement is good.
Strength of the gesso depends on the area of the glue bonds, not their length; stiffness depends on both. Mathematically:
Fig. 5. Glue bond area derived from Marion E Mecklenburg, "Some Mechanical and Physical Properties of Gilding Gesso," figs. 7, 8, elsewhere in this volume.
The expression A/Amax really refers to summed areas across an imaginary fracture plane. It will be the product not only of the average bond area of each particle but also the fraction of particles usefully bonded. This may fall to 1/2 given the realignment of particles between gel and dry stages (see fig. 4). I have derived values for A/Amax from Mecklenburg's data via equations 6, 9, and 10, shown in figure 5. The estimate from elasticity (E) is probably too low since it ignores bending of the glue bonds, and the estimate from strength (S) too high since crack growth is arrested better in gesso than pure glue. By about 94% PVC, there is very little bonding. Vicker's hardness tests made on my experimental gessoes confirm the transition at 93% PVC but show measurable bonding right up to 99% PVC. The inflections labeled 1 and 2 in figure 5 can be explained as follows: (1) Glue thickness on 1 gm particles is about 10 nm. This is in the range of the strongly adhered layer found for most binder/particle combinations, 0.5 nm to 50 nm.7 The glue will not flow enough to bridge particles. (2) Adjacent calcite polyhedra have bonded facet to facet wherever aligned favorably. More glue fills misaligned particles only slowly. If facets average about 60° in each direction, then for each particle A/Amax ~0.25, the plateau value in figure 5, and half of these are aligned favorably, so A/Amax ~0.12 at inflection 2.
Even clearcole recipes with enough glue to make solid gesso do not do so. Critical pigment volume concentration (CPVC, the PVC at which particles are just filled by a binder like oil) lies in the range of 45%-65% PVC for most whitings. Most paints near CPVC show 3 to 300 times the stiffness of the binder alone.8 In contrast, Mecklenburg's clearcole, near CPVC at 58% PVC, shows a stiffness only marginally higher than the glue. One can, therefore, consider the clearcole as either a reinforced polymer with added voids that reduce stiffness or more directly as particles held together by a binder lattice.
Drying strain is that small fraction of total shrinkage of the
gel unresolved by plastic flow. The :measured residual strains in
gesso (see table 2) are around 0.16% for 90% PVC gesso. Only 70% of
this strain occurs before exposure to 95% RH, that is 0.11% drying
strain (see fig. 3). This implies 3.2% drying
strain in the glue, which represents strain from 93% RH to 50% RH.
All drying shrinkage from wetter stages must be lost. Given the
value of a at 90% PVC by equation 8, a general expression for drying
strain  0, which can be traced to PVC, is
0, which can be traced to PVC, is
Gilding stipulates that intermediate layers be applied thinly, after the last layer is firm but still dark and cool. The glue will be gelled but not much reduced in water content. Voids will not have opened. The new layer will not lose glue to the layer below, so multiple layers of a gesso will form a uniform layer top to bottom. Thus the experimental data from single cast films should be representative. Multiple thin layers are simply a practical way to build level gesso and to avoid settling of whiting.
With conventional symbols-where S is stress,  is strain, and
E is modulus of elasticity-the macroscopical model becomes:
is strain, and
E is modulus of elasticity-the macroscopical model becomes:
The total strain at some RH and some time ( RH,t) contains the following terms:
RH,t) contains the following terms:
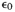 - Initial
drying strain of the gesso, at the RH of fabrication.
- Initial
drying strain of the gesso, at the RH of fabrication.
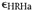 - Annealing
shrinkage of gesso due to exposure to high RH.
- Annealing
shrinkage of gesso due to exposure to high RH.
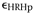 - Plastic
(irreversible) stretching of the gesso at high RH, due to wood
expansion and softening of the glue binder. This probably overrides
annealing shrinkage.
- Plastic
(irreversible) stretching of the gesso at high RH, due to wood
expansion and softening of the glue binder. This probably overrides
annealing shrinkage.
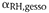 - Shrinkage
coefficient of gesso.
- Shrinkage
coefficient of gesso.
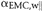 - Shrinkage
coefficient of wood parallel to the direction considered.
- Shrinkage
coefficient of wood parallel to the direction considered.
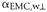 - Shrinkage
coefficient of wood perpendicular to the direction considered.
- Shrinkage
coefficient of wood perpendicular to the direction considered.
 -
Poisson ratio for gesso-that is, the fractional strain perpendicular
to the direction of applied strain (for example, at low RH the gesso
is compressed across the grain, so it bulges along the grain).
-
Poisson ratio for gesso-that is, the fractional strain perpendicular
to the direction of applied strain (for example, at low RH the gesso
is compressed across the grain, so it bulges along the grain).
 p,t - Plastic, nonrecoverable stress
relaxation, or flow. Considered a change in strain.
p,t - Plastic, nonrecoverable stress
relaxation, or flow. Considered a change in strain.
EMC - Equilibrium moisture content of the wood, dependent on RH.
Fig. 6. Predicted strain in the glue bonds for an 85% PVC gesso on wood, as humidity changes.
The microscopical model predicts values of  0
and
0
and  RH for the gesso. Wood behavior is available
from the Wood Handbook. Leaving high humidity damage
aside, total strain in the gesso has been calculated by equations
13, 11, and 8. This in turn has been converted to total strain on
the glue bonds by equation 8, since it is this strain that
determines fracture. Figure 6 plots strain as a function of RH for a
gesso of 85% PVC, manufacture at 50% RH, and quarter-cut wood, so
RH for the gesso. Wood behavior is available
from the Wood Handbook. Leaving high humidity damage
aside, total strain in the gesso has been calculated by equations
13, 11, and 8. This in turn has been converted to total strain on
the glue bonds by equation 8, since it is this strain that
determines fracture. Figure 6 plots strain as a function of RH for a
gesso of 85% PVC, manufacture at 50% RH, and quarter-cut wood, so

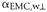 = 0.15.
Shrinkage of the wood along the grain is ignored. On inert
substrates like glass, strain rises modestly with low RH. On wood,
along; the grain, and a Poisson ratio of 0.1, stress drops ,with low
RH. A ratio of 0.1 occurs in another hard porous
material-concrete-at low strain, although 0.3 is typical of most
solids, and would give a line that drops near zero at low RH.9 Generally, strain along the grain is either
unaffected or reduced by low RH. Strain across the grain changes
much more dramatically.
= 0.15.
Shrinkage of the wood along the grain is ignored. On inert
substrates like glass, strain rises modestly with low RH. On wood,
along; the grain, and a Poisson ratio of 0.1, stress drops ,with low
RH. A ratio of 0.1 occurs in another hard porous
material-concrete-at low strain, although 0.3 is typical of most
solids, and would give a line that drops near zero at low RH.9 Generally, strain along the grain is either
unaffected or reduced by low RH. Strain across the grain changes
much more dramatically.
Fig. 7. Predicted strain in the glue bonds of gesso on wood at 20% RH, as PVC changes.
Figure 7 graphs the effect of changing the gesso recipe (PVC) on the strain, assuming manufacture at 50% RH and a drop to 20% RH. It becomes clear that whereas typical intermediate recipes (80%-90% PVC) reduce glue tension below 4% along the grain, they do so at the cost of well over 5% compression across the grain. Figure 7 also shows that clearcole recipes neatly match the movement of wood across the grain, thereby reducing shear stresses at the clearcole/ wood interface and keeping it at the clearcole/ intermediate interface. Thus gesso delaminates at this interface not simply because it is weaker but also because shear strains are higher.
Since gilding generally does not buckle along the grain, it must compress as calculated. In macroscopical dimensions, this compression is about 1% for most woods but may rise to 3% for tangential cut oak. Furthermore, since gilding frequently shows no tension cracking along the grain, this compression usually recovers elastically. Some of it may result from direct bond compression, but much of it must result from bond bending--that is, "scissoring" of the lattice. Herein lies the greatest advantage of the glue lattice: compressibility. Solid, stiff coatings like old oil paint cannot match this behavior; hence, there are more frequent cracks along the grain.
If strain is all that matters, figure 6 suggests that low humidity is not a problem and that cracks are much more likely along the grain. Neither is true. The answer lies in equation 12 for stress and the value of stiffness, E.
Fig. 8. The visco-elastic response of glue. Sources: (curve shale) 1. V Yannas, "Collagen and Gelatin in the Solid State, " Journal of Macromolecular Science-Reviews in Macromolecular Chemistry C7, no. 1 (1972): 86; (time calibration) E. Bradbury and C. Martin, "Mechanical Properties and Structure of Gelatin Films," Proceedings of the Royal Society A214 (1952): 185; J. Eliassaf and E R. Eirlch, "Creep Studies on Gelatin at 100% Relative Hunt idity," Journal of Applied Polymer Science 4, no. 11 (1961)); 201; and Marion E Mecklenburg, "The Effects of Atmospheric Moisture on the Mechanical Properties of Collagen sunder Equilibrium Conditions," in Preprints of Papers Presented at the Sixteenth Annual Meeting (New Orleans: American Institute for Conservation, 1988), p. 240.
Stiffness E is not a constant. Like many polymers, gelatin's log E can be plotted on a master curve that shows regions of glassy transition and rubbery behavior (fig. 8). The horizontal axis can be either log (time), temperature, or plasticizer concentration, such as water. If the glue is strained quickly enough or dry enough, it acts as a glassy polymer, with a stiffness of ~5 GPa. In these conditions, stress reaches the breaking point (~100 MPa) at a strain of only ~2%. The strains predicted by the gesso model far exceed these Values; however, once into transition, gelatin ran elongate by 10%-20%, and in its rubbery Phase cant reach more than 200%! Obviously gesso will survive easily as long as strain is applied in the transition or rubbery regions. The stress relaxation data of figures 3 and 8 (curve A) indicate transition starts at about three months at 50% RH 1, This is midway between the hygrometric halftimes of gilded objects (see table 1). Thus, tension at high humidity across the grain (see fig. 6) can be accommodated because high humidity reduces transition time to under an hour, whereas low humidity increases transition times to many months. Unfortunately, the horizontal axis For figure 8 is known precisely only for temperature and the scales of time shown are my best estimate based on the temperature data of I.V Yannas, all the humidity data available, and an equivalence of 5°c=one decade time.10 Precise times must await new data.
Fig. 9. Idealized stress strain-curves for glue at 50% RH, 21°C. Sources: E. Bradbury and C. Martin, "Mechanical Properties and Structure of Gelatin Films," Proceedings of the Royal Society A214 (1952): 185; J. Eliassaf and F. R. Eirich, "Creep Studies on Gelatin at 100% Relative Humidity," Journal Applied Polymer Science 4, no. 11 (1960): 201; and Marion F. Mecklenburg, "The Effects of Atmospheric Moisture on the Mechanical Properties of Collagen under Equilibrium Conditions," in Preprints of Papers Presented at the Sixteenth Annual Meeting (New Orleans: American Institute for Conservation, 1988), p. 240.
The transitions in gelatin are even more complicated than simple polymers. Mecklenburg has shown that tensile tests carried out over a day or so show two phases, simplified in figure 9 as two linear sections A and B. Phase A behaves with glassy stiffness up to a critical stress, then yields to Phase B. Phase B is in transition when tested over hours and days (at 5%-0% RH) but acts glassy when stressed in one second. Both phases recover elastically. J. Eliassaf and E R. Eirich found the same two phases in the rubbery regime.11 Figure 8 represents my best estimate of phase B response from these two studies. Phase B is critical because even at low humidity its transition begins in hours, rather than the months of phase A.
We can now make better sense of the drying stress value in figure 3, about 0.8 MPa. Given the ratio A/Amax. ÷ 0.04 for this gesso (90% PVC; see fig. 5), the glue bond stress must be 20 MPa. The glue bonds have a drying strain of 3.2% (see fig. 6). This, stress/strain condition is shown by the star in figure 9. It sits in the region of phase B transition behavior because most strain entered during damp conditions, where transition times are under an hour. Hence, drying glue easily incorporates 3%-4% strain without breaking.
Calcite particles (natural ground and precipitated) ;ire roughly spherical with uniform surface chemistry as assumed in the model (see fig. 4). Kaolin is neither. Its lamellar particles will align themselves like fallen leaves as the gesso dries. The edges and faces differ in their surface chemistry; indeed, some water-soluble binders appear to migrate to the particle edges.12 Thus the glue lattice in a kaolin gesso would cleave more easily and be less compressible.
Another important characteristic of whitings is their particle size distribution. A mix of large and small particles packs more closely, and porosity can drop to as little as 15% from the usual 40%. Hence, mixing kaolin, which is always fine (50% under 1 gm) with natural calcium carbonates, which are usually several times coarser (typically under 50% 10 gm), would yield a less extensible gesso.13
A model has been developed for the mechanical properties of gesso. It predicts expansion coefficients -by predicting the bond length of the glue lattice that holds whiting particles in place. It is this lattice that allows gesso to compress remarkably across the grain without buckling.
Internal strain of the glue bonds has been modeled. Drying strain of 3%-4% tension forms without cracks because most tension enters while the glue is partly rubbery. Subsequent strain fluctuations are dangerous only if applied in glue's glassy phase; that is, humidity fluctuations are dangerous only if applied too fast. The gold leaf plays the important role of delaying humidity response of the object long enough for the glue to lose its glassy response. Strain in gesso is highest across the grain at high humidity, but it is harmless because glassy response lasts less than a day. Low humidity is dangerous because glassy behavior persists for months. At low humidity, the gesso is under tension only along the grain, so it cracks across the grain. Since cracks in gilding are remarkably straight and evenly spaced, they probably result from fatigue, that is, small growth at each cycle.
Partly gilded pieces, such as frames, seats, and tabletops, suffer humidity fluctuation only because the backsides are bare. "Completely" gilded pieces, such as chair legs, respond to the extent that their end grain is exposed or the leaf abraded. If such surfaces were sealed well, the artifact would be immune to all normal humidity fluctuations. In the long run, I think that such actions would benefit the gilding much more than small adjustments in gesso recipe.
Tradition has already narrowed down the ideal intermediate layer as much as possible that is, between 80% and 90% PVC. The tradeoff is compression sensitivity across the grain at 90% PVC or tension sensitivity along the grain at 80% PVC. Suffice it to say that over the centuries gilders developed a coating hard enough for burnishing yet flexible enough to follow wood's movements, given time. Gold leaf, a perfect vapor barrier, gave that margin of time better than any other finish.
1. Claudia Deschu, "An Overview of Gilded Picture Frames (with an Emphasis on Stress Cracking in Gesso)," in Papers, Art Conservation Training Programs Conference (Cambridge, Mass.: Center for Conservation and Technical Studies, Harvard University Art Museums, 1984), pp. 39-54.
2. Kozo Sato, "The Internal Stress of Coating Films," Progress in Organic Coatings 8 (1980): 143-60.
3. T. Baumeister, E. A. Avalone, and T. Baumeister III, Mark's Standard Handbook for Mechanical Engineers (8th ad.; New York: McGraw-Hill Book Co., 1978), pp. 12-75; J. Crank, The Mathematics of Diffusion (2d ad.; Oxford: Clarendon Press, 1975), p. 239.
4. Robert F. Hall, "Calcium Carbonate, Natural," in Pigment Handbook, vol. 1, Properties and Economics, ed. Temple C. Patton (New York: John Wiley and Sons, 1973), p. 110.
5. In contrast, see Marion F. Mecklenburg, "Some Mechanical and Physical Properties of Gilding Gesso," elsewhere in this volume. His restrained hardwhite lost stress after high RI-1, because his samples were under a modest applied stress that erased the annealing strain as well as some of the applied strain by plastic flow.
6, Fred B. Stieg, "Pigment/Binder Geometry," in Pigment handbook, vol. 3, Characterization and Physical Relationships, ed. Temple C. Patton (New York: John Wiley and Sons, 1973), p. 205; A. S. Marshall and S. E. B. Petrie, "Thermal Transitions in Gelatin and Aqueous Gelatin Solutions," Journal of Photographic Science 28 (1980): 128-34.
7. A. Zosel, "Mechanical Behavior of Coating Films," Progress in Organic Coatings 8 (1980):, 47-79.
8. Stieg, "Pigment/Binder Geometry," p. 207; Zosel, "Mechanical Behavior," p. 67.
9. Forest Products Laboratory, Wood Handbook: Wood as an Engineering Material (rev. ed.; Washington, D.C.: Department of Agriculture, 1987), chap. 3 p. 11, chap. 14 p. 41; Baumeister Avalone, and Baumeister, Mark's Standard Hang book chap. 5 p. 16.
10. Zosel, "Mechanical Behavior," p. 59; 1. V. Yannas, "Collagen and Gelatin in the Solid State," Journal o f Macromolecular Science-Reviews in Macromolecular Chemistry C7, no. 1 (1972): 49-104; E. Bradbury and C. Martin, "Mechanical Properties and Structure of Gelatin Films," Proceedings of the Royal Society A214 (1952): 183-92; J. Eliassaf and F. R. Eirich, "Creep Studies on Gelatin at 100% Relative Humidity," Jour- nal of Applied Polymer Science 4, no. 11 (1960): 200-202; Marion F. Mecklenburg, "The Effects of Atmospheric Moisture on the Mechanical Properties of Collagen under Equilibrium Conditions," in Preprints o f Papers Presented at the Sixteenth Annual Meeting (New Orleans: American Institute for Conservation, 1988), pp. 231-44.
11. Mecklenburg, "Effects of Atmospheric Moisture," pp. 231-44; Eliassaf and Eirich, "Creep Studies," pp. 200-202.
12. Hall, "Calcium Carbonate," p. 115; Philip F. Woerner, "Calcium Carbonate, Synthetic," in Pigment Handbook, 3:125; D. H. Solomon and D. G. Hawthorne, Chemistry of Pigments and Fillers (New York: John Wiley and Sons, 1983), p. 97; Lamar E. Brooks and H. H. Morris, "Aluminum Silicate, Kaolin," in Pigment Handbook, 3:209; Solomon and Hawthorne, Chemistry of Pigments and Fillers, pp. 10-11; M. Parpaillon, G. E. Engstrom, I. Pettersson, I. Fineman, S. E. Svanson, B. Dellenfalk, and M. Rigdahl, "Mechanical Properties of Clay Coating Films Containing Styrene-Butadiene Copolymers," Journal of Applied Polymer Science 30 (1985): 581-92.
13. C. R. Hegedus and A. T. Eng, "Coating Formulation and Development Using Critical Pigment Volume Concentration Prediction and Statistical Design," Journal o f Coatings Technology 60, no. 767 (December 1988): 77-87; Brooks and Morris, "Aluminum Silicate, Kaolin," p. 209; Woerner, "Calcium Carbonate, Synthetic," p. 125.
Stefan Michalski received a Bachelor of Science in physics and mathematics from Queen's University at Kingston, Canada, in 1972. He trained as artifacts conservator at Queen's program from 1977 to 1979. He has published articles on suction tables, light damage, museum lighting, deterioration of paintings, and cleaning of painted surfaces. He serves as adviser to Canadian museums, galleries, and archives on environmental control and is currently senior conservation scientist, Canadian Conservation Institute, Communications Canada, Ottawa.
Courtesy of Sound View Press, publisher of Guilded Wood: Conservation and History. This and other scholarly references on American art are available at http://www.falkart.com